
|
 
  
 |
Eccentricity of Orbiting PlanetsEllipses in the real world
The eccentricy of an ellipse is a measure of how nearly circular the ellipse is. Eccentricity is found by the following formula
eccentricity = c/a
Use the formula for eccentricity to determine the eccentricity of the imaginary planet's orbit.
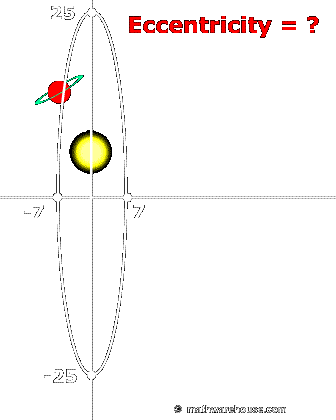
Use the eccentricity of the ellipse to determine where the focus (sun) is in the imaginary example below
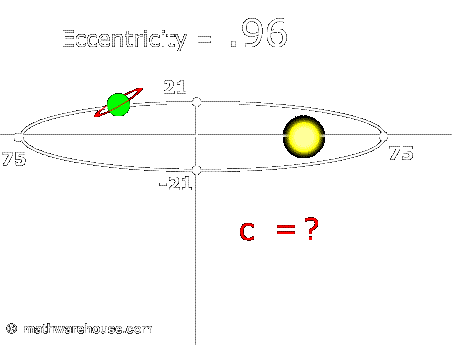
The eccentricity of the orbit of the planet below is 0.8 and the value of c is 20. What is the value of this planet's semi-major axis (semi-major axis = a in ellipse's equation)?
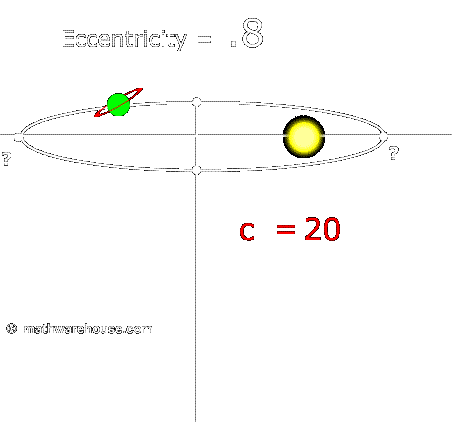
Eccentricities and Orbits of Real Planets in our Solar System
The eccentricity of mars is.093 and the value of c is 132,000,000 miles. What is the value of Mar's semi-major axis (semi-major axis = a in ellipse's equation)?
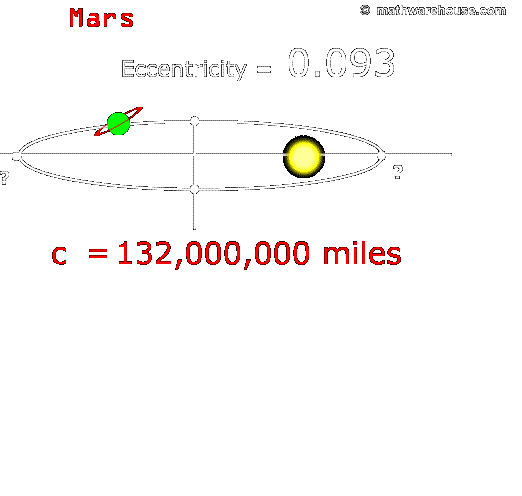 |