-
Related:
- Equation of Ellipse
- Major Axis of Ellipse
- Minor Axis of Ellipse
- Vertices
- Co-vetices
- focus of an ellipse
- Is a circle an ellipse?
- Eccentricty of Ellipse
- area of an ellipse
- Orbits of Planets as ellipses
- Translate ellipse
- images
- Worksheet Version of this Web page (same questions on a worksheet)
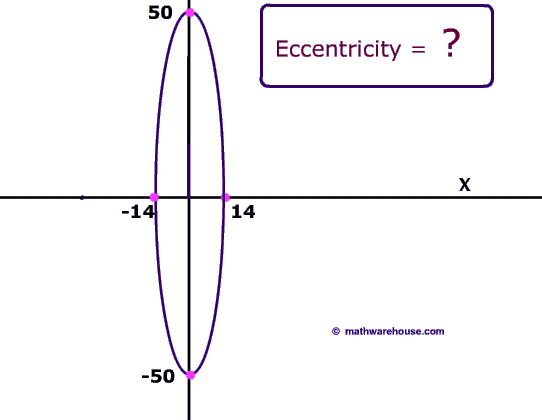
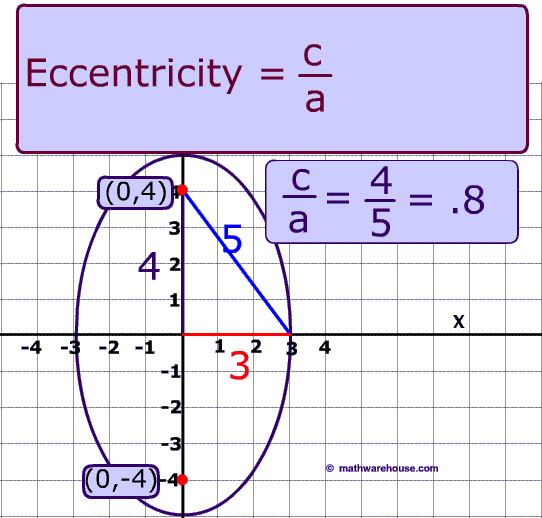
The eccentricity of an ellipse is a measure of how nearly circular the ellipse. Eccentricity is found by the following formula eccentricity = c/a where c is the distance from the center to the focus of the ellipse a is the distance from the center to a vertex
Formula for the Eccentricity of an Ellipse
The special case of a circle's eccentricity
A circle is a special case of an ellipse. Analogous to the fact that a square is a kind of rectangle, a circle is a special case of an ellipse. In terms of the eccentricity, a circle is an ellipse in which the eccentricity is zero.
Practice Problems