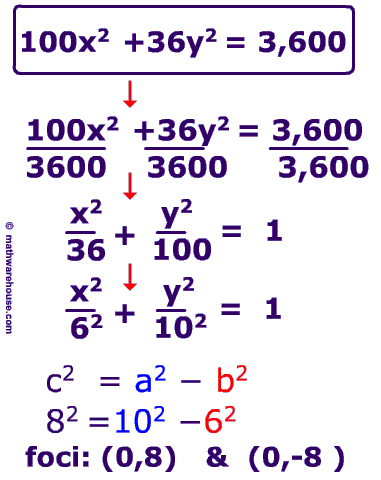What is a focus of an ellipse?
An ellipse has 2 foci (plural of focus). In the demonstration below, these foci are represented by blue tacks 
. These 2 foci are fixed and never move.
Now, the ellipse itself is a new set of points. To draw 
this set of points and to make our ellipse, the following statement must be true:
if you take any point on the ellipse, the sum of the distances to those 2 fixed points ( blue tacks ) is constant. We explain this fully here.
Full lesson on what makes a shape an ellipse here .
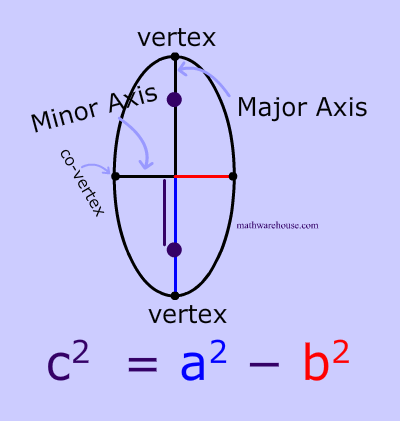
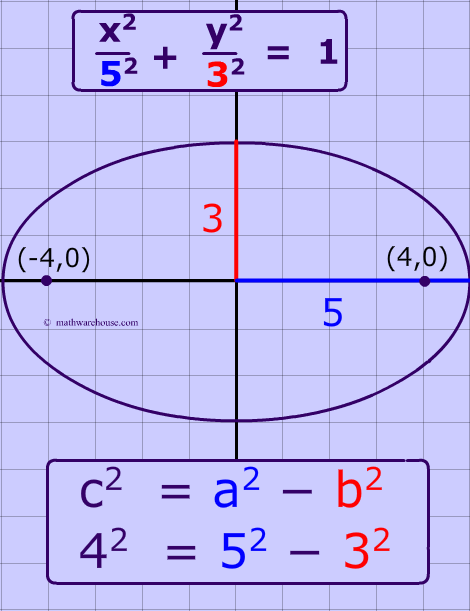
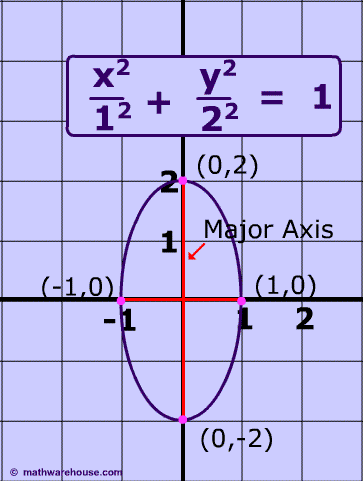
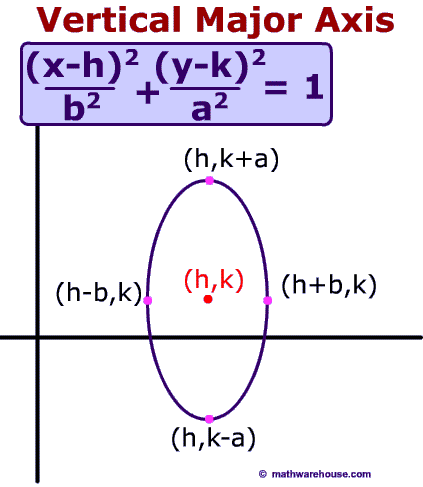
Formula for the focus of an Ellipse
The formula generally associated with the focus of an ellipse is $$ c^2 = a^2 - b^2$$ where $$c $$ is the distance from the focus to center, $$a$$ is the distance from the center to a vetex and $$b$$ is the distance from the center to a co-vetex .
