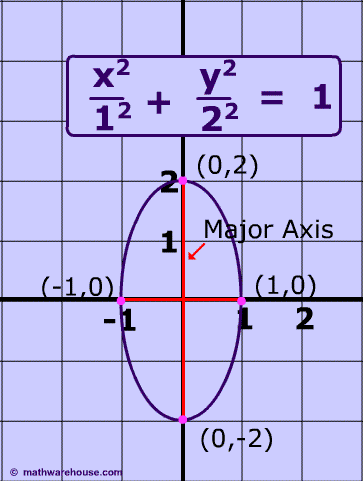
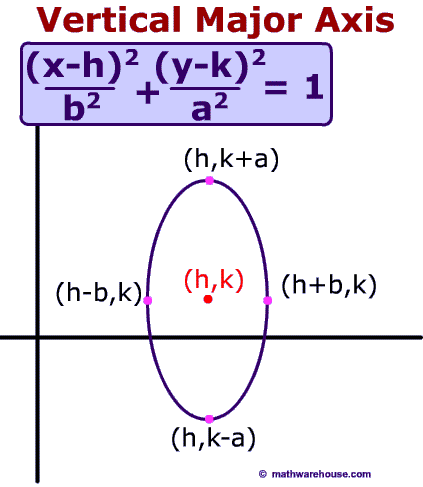
What makes an ellipse ?
An ellipse is based around 2 different points. These 2 points are fixed and never move. In the demonstration below, we use blue tacks 
to represent these special points. Mathematicians have a name for these 2 points. We call each one a focus of the ellipse (link) .
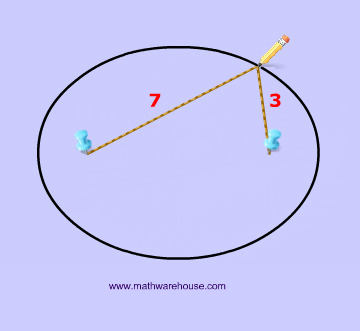
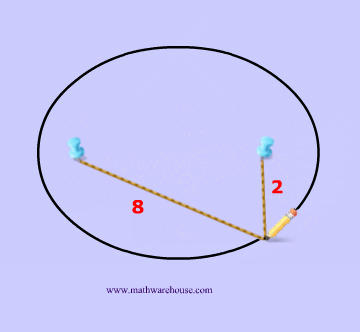
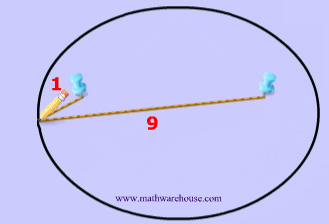
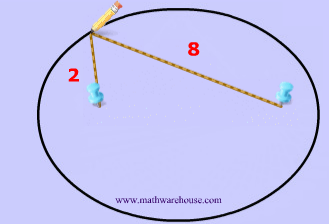
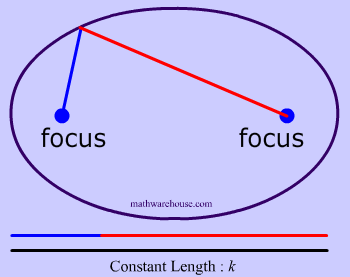
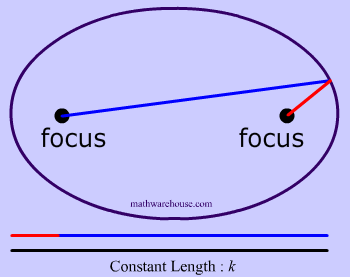
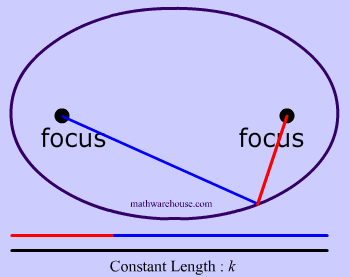
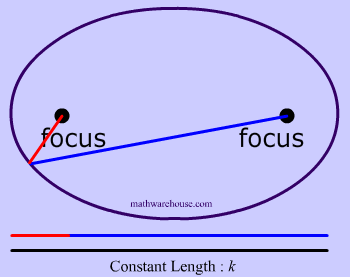
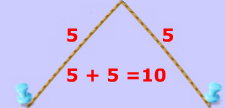
Now that we have these two points, we are going to need a constant. This constant will obviously never change, and in the diagrams below the constant is represented by how long the yarn is. For instance, the yarn in diagrams 1 and 2 below has the constant length of 10.
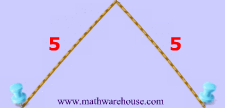
The ellipse itself is a new set of points.
To create this set of points and to make our ellipse, the following statement must be true: the sum of the distances from anywhere on the ellipse to those 2 points ( blue tacks ) must be that constant number . This may sound like a lot of mathematical mumbo-jumbo. It's easier to understand this by looking at Diagrams 3- 7 .
That last sentence simply means that we draw an ellipse by adding up the 2 parts of the yarn to get the whole length of the yarn. The length of the yarn is constant and does not change.
Constant Length
