Methods to Solve Quadratic Equations
A quadratic equation is an equation that can be written as ax ² + bx + c where a ≠ 0.
In other words, a quadratic equation must have a squared term as its highest power.
Below are the 4 methods to solve quadratic equations. Click on any link to learn more about a method.
Examples of quadratic equations
$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + 5 $$
Non Examples
$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$
The solution of a quadratic equation is the value of x when you set the equation equal to zero.
Graphically, since a quadratic equation represents a parabola. The solution (for real numbers) is where the parabola cross the x-axis.
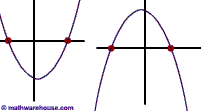
i.e. When you solve the following general equation: 0 = ax² + bx + c.
Parabola Gif













