Examples
Example 1
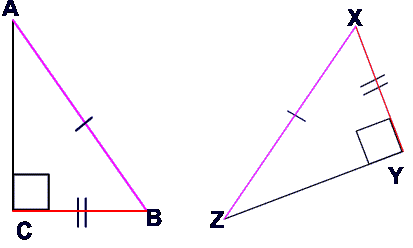
Given:
$ \overline{AC} \cong \overline{ZY}
\\
\overline{AB} \cong \overline{XZ}
\\
m\angle ACB = m\angle ZYX = 90^{o}
$
Prove:
$ \triangle ACB \cong \triangle ZYX $
| Statement | Reason |
|---|---|
| $$ \angle ACB $$ and $$ \angle ZYX $$ are both right angles | Given |
| $$ \triangle ABC$$ and $$ \triangle XYZ$$ are right triangles | Right Triangles have a right angle |
| $$ \overline{AB} \cong \overline{XZ} $$ | Given |
| $$ \overline{AC} \cong \overline{ZY} $$ | Given |
| $$ \triangle ACB \cong \triangle ZYX $$ | Hypotenuse Leg Theorem |
Example 2
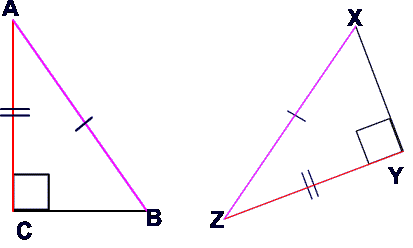
The following proof simply shows that it does not matter which of the two (corresponding) legs in the two right triangles are congruent.
-
![triangle symbol]()
ABC and
![triangle symbol]()
XZY are right triangles since they both have a right angle
- AB = XZ (hypotenuse) reason: given
- CB = XY (leg) reason: given
-
![triangle symbol]()
ABC
![congruent symbol]()
![triangle symbol]()
XYZ by the hypotenuse leg theorem which states that two right triangles are congruent if their hypotenuses are congruent and a corresponding leg is congruent.
ABC and
