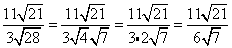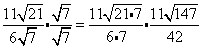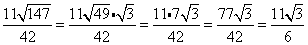1. Home
  2. Radicals Home

How to Rationalize the Denominator

Examples, formula and the Steps!

Why do we rationalize the denominator?

The most important reason, usually is "Because your teacher told you!"

There is nothing mathematically wrong with something like $$ \frac{3}{\red{ \sqrt{5}}} $$ or with any fraction that has a radical in its denominator

Just like in elementary school when you were probably told that fractions like $$\frac{7}{2} $$ 'bad' (or 'improper' in this case), having a radical in the denominator is not actually mathematically 'wrong'.

A historical reason: Before we had calculators that could compute radicals , we had to to calculate the value of radicals by hand, and it's much easier to do that when the radical is in the numerator.

Nowadays: There are two reasons why we still rationalize the denominator. Since most types of expressions and equations have a standard form, such a form was needed for rational expressions with radicals. And since we had historically rationalized the denominators due to a lack of calculators, this form became the standard one.

The good news: it's usually not very difficult to rationalize the denominator, and you can always double check your work with our calculator.

First, some background knowledge

In order to rationalize the denominator, you must multiply the numerator and denominator of a fraction by some radical that will make the 'radical' in the denominator go away.

Below is some background knowledge that you must remember in order to be able to understand the steps we are going to use.

Multiplying a fraction by 1

Remember that you can create an equivalent fraction by multiplying your original fraction ($$ \frac{2}{3} $$ in the example below) by 1, $$ \red{\frac{5}{5} }$$ , or by $$ \frac{7}{7} $$ or by any form of 1 as a fraction

$ \frac{2}{3} \cdot \red{\frac{5}{5} } = \frac{10}{15} $

Multiply Radicals

The product of two square roots is the square root of the products

(In other words you can multiply two square roots and put them under the same radical as shown below)

$ \sqrt{2} \sqrt{3} = \sqrt{6} $

Full lesson on multiplying square roots.

How to Rationalize the Denominator PowerPoint

Examples of rationalizing the denominator

Example 1 - Simplified Denominator

Rationalize the denominator of $$ \frac{2}{\sqrt{3}} $$

Note: this first example is the easiest type--It has a simplified denominator with no variables. Scroll down the page for more difficult examples

Step 1) Multiply the numerator and denominator of the original fraction $$ \left ( \frac{2}{\sqrt{3}} \right ) $$ by a number that will make the radical in the denominator 'go away' $$ \red{\frac{\sqrt{3}}{\sqrt{3}}}$$

$$ \frac{2}{\sqrt{3}} \cdot \red{\frac{\sqrt{3}}{\sqrt{3}}} $$
Step 2) Simplify
$$ \frac{2 \sqrt{3}}{\sqrt{3}\sqrt{3}} = \frac{2 \sqrt{3}} { \sqrt{9}} = \frac{2 \sqrt{3}} { \red{\sqrt{9}}} = \frac{2 \sqrt{3}} { \red{3}} $$
Example 2 - Denominator not Simplified

Rationalize $$ \frac{3}{ 5 \sqrt{8} }$$

Step 1) Simplify the denominator

$$ \frac{3}{ 5 \red{\sqrt{8}} } = \frac{3}{ 5 \red{\sqrt{4} \sqrt{2}} } = \frac{3}{ 5 \cdot \red{2 }\sqrt{2} } = \frac{3}{ 10 \sqrt{2} } $$
Step 2) Multiply the numerator and denominator by a number that will make the radical in the denominator 'go away' : $$ \red{ \frac{ \sqrt{2} }{\sqrt{2}}} $$
$$ \frac{3}{ 10 \sqrt{2} } \cdot \red{ \frac{ \sqrt{2} }{\sqrt{2}}} $$

Step 3) Simplify

$$ \frac{3 \sqrt{2}}{ 10 \red{\sqrt{2 }\sqrt{2} }} = \frac{3 \sqrt{2}}{ 10 \cdot \red{2}} = \frac{3 \sqrt{2}}{ 20} $$
Example 3 - Conjugates
(more on rationalizing denominators with conjugates)

Rationalize $$ \frac{3}{2 + \sqrt{5}} $$

Step 1) Simplify the square root in the denominator (if possible)

$$ \sqrt{5} $$ is already simplified, so nothing to do here
Step 2) Multiply the numerator and denominator by the denominator's conjugate $$ 2 \red{-} \sqrt{5} $$
$$ \frac{3}{2 + \sqrt{5}} \red{ \frac{2 - \sqrt{5}} {2 - \sqrt{5}}} = \frac{3 (2 \red{-} \sqrt{5} )} { (2\red{+} \sqrt{5} )(2\red{-} \sqrt{5} ) } \\ = \frac{ 6 -3\sqrt{5} } {4 \red{+} 2\sqrt{5} \red{-} 2\sqrt{5}+ 5} = \frac{ 6 -3\sqrt{5} } {4 \cancel { \red{+}2\sqrt{5} \red{-} 2\sqrt{5} } + 5 } \\ = \frac{ 6 -3\sqrt{5} } {4 + 5 } = \frac{ 6 -3\sqrt{5} } { 9 } $$

Step 3) Simplify

$$ \frac{ 6 -3\sqrt{5} } { 9 } = \frac{ \red{3}(2 -1\sqrt{5}) } { \red{3}(3) } \\ \frac{ \red{\cancel{3}}(2 -1\sqrt{5} ) } { \red{\cancel{3} } (3 ) } = \frac{ (2 - \sqrt{5} )} { 3 } $$

Practice Problems

Problem 1

Rationalize $$ \frac{3}{ \sqrt{7}} $$

This problem is like example 1 since its denominator is already simplified.

Step 1

Multiply the numerator and denominator of the original fraction $$ \frac{3}{ \sqrt{7}} $$ by a number that will make the radical in the denominator 'go away' $$ \red{ \frac{\sqrt{7}}{ \sqrt{7}} } $$

$$ \frac{3}{ \sqrt{7}} \cdot \red{ \frac{\sqrt{7}}{ \sqrt{7}}} $$
Step 2

Simplify

$$ \frac{3 \sqrt{7} }{ \sqrt{7} \cdot \sqrt{7}} = \frac{3 \sqrt{7} }{ 7} $$
Problem 2

Rationalize $$ \frac{ 2}{3 \sqrt{11}} $$

This problem is like example 1 since its denominator is already simplified.

Step 1

Multiply the numerator and denominator of the original fraction

$$ \frac{ 2}{3 \sqrt{11}} $$ by a number that will make the radical in the denominator 'go away' $$ \red{ \frac{\sqrt{11}}{ \sqrt{11}} } $$
$$ \frac{ 2}{3 \sqrt{11}} \cdot \red{ \frac{\sqrt{11}}{ \sqrt{11}} } $$
Step 2
Simplify
$$ \frac{ 2}{3 \sqrt{11}} \cdot \red{ \frac{\sqrt{11}}{ \sqrt{11}} } = \frac{ 2 \sqrt{11} }{3 \cdot 11} = \frac{ 2 \sqrt{11} }{33} $$
Problem 3

Rationalize $$ \frac{5}{6 \sqrt{27}} $$

This problem is like example 2 since its denominator is not simplified.

Step 1

Simplify the denominator

$$ \frac{5}{6 \sqrt{27}} = \frac{5}{6 \sqrt{9} \sqrt{3}} = \frac{5}{6 \cdot 3\sqrt{3}} \\ = \frac{5}{ 18\sqrt{3}} $$
Step 2

Multiply the numerator and denominator of the fraction

$$ \frac{5}{ 18\sqrt{3}} $$ by a number that will make the radical in the denominator 'go away' $$ \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
$$ \frac{5}{ 18\sqrt{3}} \cdot \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
Step 3
Simplify
$$ \frac{5 \sqrt{3} }{ 18 \red{\sqrt{3} \sqrt{3}} } = \frac{5 \sqrt{3} }{ 18 \red{\sqrt{9} }} = \frac{5 \sqrt{3} }{ 18 \cdot \red{3 }} \frac{5 \sqrt{3} }{ 54 } $$
Problem 4

Rationalize $$ \frac{ 3 \sqrt{2}}{ 7 \sqrt{12}} $$

This problem is like example 2 since its denominator is not simplified.

Step 1

Simplify the denominator

$$ \frac{ 3 \sqrt{2}}{ 7 \red{\sqrt{12} }} = \frac{ 3 \sqrt{2}}{ 7 \cdot \red{\sqrt{4}\sqrt{3} }} = \frac{ 3 \sqrt{2}}{ 7 \cdot \red{2 }\sqrt{3}} = \frac{ 3 \sqrt{2}}{ \red{14 }\sqrt{3}} $$
Step 2

Multiply the numerator and denominator of the fraction

$$ \frac{ 3 \sqrt{2}}{ 14 \sqrt{3}} $$ by a number that will make the radical in the denominator 'go away' $$ \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
$$ \frac{ 3 \sqrt{2}}{ 14 \sqrt{3}} \cdot \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
Step 3
Simplify
$$ \frac{ 3 \sqrt{2}}{ 14 \sqrt{3}} \cdot \red{ \frac{\sqrt{3}}{ \sqrt{3}} } = \frac{ 3 \red{\sqrt{2} \sqrt{3}}}{ 14 \red{\sqrt{3} \sqrt{3}} } = \frac{ 3 \red{\sqrt{2 \cdot 3}}}{ 14 \cdot \red{3} } = \frac{ \cancel{3} \red{\sqrt{6}}}{ 14 \cdot \cancel{ \red{3} }} = \frac{ \sqrt{6} }{14} $$
Problem 5

Rationalize $$ \frac{ 5 \sqrt{6} }{ 2 \sqrt{27} } $$

This problem is like example 2 since its denominator is not simplified.

Step 1

Simplify the denominator

$$ \frac{ 5 \sqrt{6} }{ 2 \sqrt{27} } = \frac{ 5 \sqrt{6} }{ 2 \red{\sqrt{9} \sqrt{3} } } = \frac{ 5 \sqrt{6} }{ 2 \cdot \red{3 \sqrt{3} } } = \frac{ 5 \sqrt{6} }{ \red{6} \sqrt{3} } $$
Step 2

Multiply the numerator and denominator of the fraction

$$ \frac{ 5 \sqrt{6} }{ 6 \sqrt{3} } $$ by a number that will make the radical in the denominator 'go away' $$ \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
$$ \frac{ 5 \sqrt{6} }{ 6 \sqrt{3} } \cdot \red{ \frac{\sqrt{3}}{ \sqrt{3}} } $$
Step 3
Simplify
$$ \frac{ 5 \sqrt{6} }{ 6 \sqrt{3} } \cdot \red{ \frac{\sqrt{3}}{ \sqrt{3}} } = \frac{ 5 \red{ \sqrt{6 \cdot 3}} }{ 6 \red{ \sqrt{3} \sqrt{3}} } =\frac{ 5 \red{ \sqrt{18 }} }{ 6 \cdot \red{ 3} } =\frac{ 5 \red{ \sqrt{9 } \sqrt{2}} }{ 6 \cdot \red{ 3} } =\frac{ 5 \cdot \red{ 3} \sqrt{2} }{ 6 \cdot \red{ 3} } \\ =\frac{ 5 \cdot \red{ \cancel{ 3 } } \sqrt{2} }{ 6 \cdot \red{ \cancel{ 3} } } =\frac{ 5 \sqrt{2} } { 6 } $$
Problem 6

Rationalize $$ \frac{ 11 \sqrt{21} }{ 3 \sqrt{28} } $$

At first, this appears to be a problem like example 2 since its denominator is not simplified, but, if you look carefully, there's a quick way to solve this problem

Step 1

simplify the denominator

$$ \frac{ 11 \sqrt{21} }{ 3 \sqrt{28} } = \frac{ 11 \sqrt{21} }{ 3 \red{\sqrt{4} \sqrt{7}} } $$
Step 2

Do you notice anything about the numerator and the denominator that could help us?

The $$ \red{\sqrt{21}} $$ from $$ \frac{ 11 \red{ \sqrt{21}} }{ 3 \sqrt{4} \sqrt{7} } $$ can be rewritten as $$ \sqrt{7} \sqrt{ 3} $$

Step 3
Simplify
$$ \frac{ 11 \red{\sqrt{7} \sqrt{3} } }{ 3\sqrt{4} \sqrt{7} } = \frac{ 11 \cancel{ \sqrt{7}} \sqrt{3} }{ 3\sqrt{4} \cancel{ \sqrt{7}} } = \frac{ 11 \sqrt{3} }{ 3 \cdot \red{2} } = \frac{ 11 \sqrt{3} }{ 6 } $$
Step 4

This problem is like example 2 since its denominator is not simplified.

Step 1) Simplify the denominator

Step 2) Multiply the numerator and denominator by a number that will make the radical in the denominator 'go away'

Step 3) Simplify

Rationalize Denominator Widget

Simply type into the app below and edit the expression. The Math Way app will solve it form there. You can visit this calculator on its own page here.

To read our review of the Math way--which is what fuels this page's calculator, please go here.

Rationalize Denominator Calculator

Ultimate Math Solver (Free)

Free Algebra Solver ... type anything in there!