Some Necessary Background Knowledge
I. Know your Perfect Squares!
Before you learn how to simplify radicals,you need to be familiar with what a perfect square is. Also, you should be able to create a list of the first several perfect squares. This is easy to do by just multiplying numbers by themselves as shown in the table below.
| List Perfect Squares | |
|---|---|
| 2*2 | 4 |
| 3*3 | 9 |
| 4*4 | 16 |
| 5*5 | 25 |
| 6*6 | 36 |
| 7*7 | 49 |
| 8*8 | 64 |
| 9*9 | 81 |
| 10*10 | 100 |
| 11*11 | 121 |
| 12*12 | 144 |
| 13*13 | 169 |
II. You can rewrite a radical as the product of two radical factors of its radicand !
That's a very fancy way of saying that you can rewrite radicals as shown in the table below.
| Original Radical | Radical rewritten as product of factors |
|---|---|
|
|
|
|
|
|
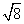
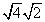
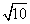
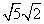
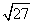
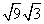
How to Simplify Radicals Steps
Let's look at
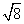to help us understand the steps involving in simplifying radicals.
Find the largest perfect square that is a factor of the radicand.
4 is the largest perfect square that is a factor of 8.
Rewrite the radical as a product of the square root of 4 (found in last step) and its matching factor(2).
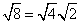
Simplify.
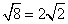
Simplify the radicals below
Problem 1
Simplify
.
Follow the steps for simplifying radicals.
Step 1Find the largest perfect square that is a factor of the radicand (72).
36 is the largest perfect square that is a factor of 72.
Step 2
![root72 = root36root2]()
Rewrite the radical as a product of the square root of 36 (found in last step) and its matching factor (2).
Step 3
![root72 = root36root2 = 6root2]()
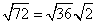
Simplify.
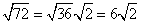
Problem 2
Simplify
.
Follow the steps for simplifying radicals.
Step 1Find the largest perfect square that is a factor of the radicand (50).
25 is the largest perfect square that is a factor of 50.
Step 2
![root50 = root25root2]()
Rewrite the radical as a product of the square root of 25 (found in last step) and its matching factor (2).
Step 3
![root25root2 = 5root2]()
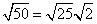
Simplify.
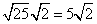
Problem 3
Simplify
.
You know the deal. Just follow the steps.
Step 1Find the largest perfect square that is a factor of the radicand (75).
25 is the largest perfect square that is a factor of 75.
Step 2
![root75 = root25root3]()
Rewrite the radical as a product of the square root of 25 (found in last step) and its matching factor (3).
Step 3
![root25root3 = 5root3]()
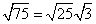
Simplify.
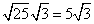
Problem 4
Simplify
.
Follow the steps for simplifying radicals.
Step 1Find the largest perfect square that is a factor of the radicand (32).
16 is the largest perfect square that is a factor of 32.
Step 2
![root32 = root16root2]()
Rewrite the radical as a product of the square root of 16 (found in last step) and its matching factor (2).
Step 3
![root16root2 = 4root2]()
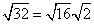
Simplify.
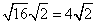
Problem 5
Simplify
.
Hopefully, by know you know how to simplify radicals.
Step 1Find the largest perfect square that is a factor of the radicand (200).
100 is the largest perfect square that is a factor of 200.
Step 2
![root200 = root100root2]()
Rewrite the radical as a product of the square root of 100 (found in last step) and its matching factor (2).
Step 3
![root100root2 = 10root2]()
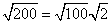
Simplify.
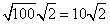
Problem 6
Simplify
.
Remember just follow the steps for how to simplify radicals.
Step 1Find the largest perfect square that is a factor of the radicand (108).
36 is the largest perfect square that is a factor of 108.
Step 2
![root108 = root36root3]()
Rewrite the radical as a product of the square root of 108 (found in last step) and its matching factor (3).
Step 3
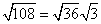
Simplify.
$$ {\sqrt{36}} \sqrt{3} = 6 \sqrt{3} $$
Problem 7
Simplify
.
Ok, this question is a trick one to see if you really understand step 1 of how to simplify radicals.
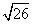cannot be simplified because this radicand (26) does not have any perfect square factors. Therefore, you cannot simplify it.
How to Simplify Radicals with Coefficients
Let's look at
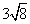to help us understand the steps involving in simplifying radicals that have coefficients. All that you have to do is simplify the radical like normal and, at the end, multiply the coefficient by any numbers that 'got out' of the square root.
Find the largest perfect square that is a factor of the radicand (just like before).
4 is the largest perfect square that is a factor of 8.
Rewrite the radical as a product of the square root of 4 (found in last step) and its matching factor(2).
Simplify.
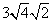
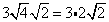
Multiply original coefficient (3) by the 'number that got out of the square root' (2).
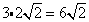
Practice Simplifying Radicals with Coefficients
Problem 8
Simplify
.
Follow the steps for simplifying radicals with coefficients.
Step 1Find the largest perfect square that is a factor of the radicand (just like before).
4 is the largest perfect square that is a factor of 20.
Step 2
![6root20 = 6root4root5]()
Rewrite the radical as a product of the square root of 4 (found in last step) and its matching factor(5).
Step 3
![6root4root5 = 6*2root5]()
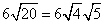
Simplify.
Step 4
![6*2root5 = 12root5]()
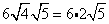
Multiply original coefficient (6) by the 'number that got out of the square root ' (2).
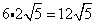
Problem 9
Simplify
.
Follow the steps for simplifying radicals with coefficients.
Step 1Find the largest perfect square that is a factor of the radicand (just like before).
16 is the largest perfect square that is a factor of 80.
Step 2
![2root80 = 2root16root5]()
Rewrite the radical as a product of the square root of 16 (found in last step) and its matching factor(5).
Step 3
![2root16root5 = 2*4root5]()
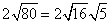
Simplify.
Step 4
![2*4root5 = 8root5]()
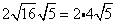
Multiply original coefficient (2) by the 'number that got out of the square root ' (2).
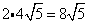
Problem 10
Simplify
.
Follow the steps for simplifying radicals with coefficients.
Step 1Find the largest perfect square that is a factor of the radicand (just like before).
25 is the largest perfect square that is a factor of 125.
Step 2
![4root125 = 4root25root5]()
Rewrite the radical as a product of the square root of 25 (found in last step) and its matching factor(5).
Step 3
![4root25root5 = 4*5root5]()
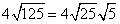
Simplify.
Step 4
![4*5root5 = 20root5]()
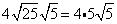
Multiply original coefficient (4) by the 'number that got out of the square root ' (5).
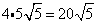
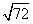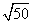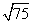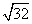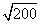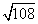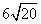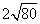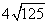