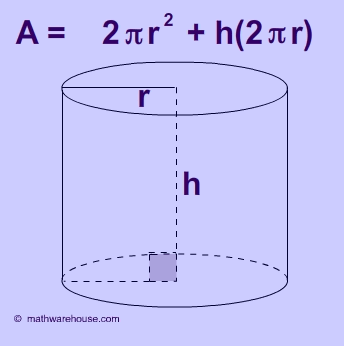-
Related Links:
- Multiplying Monomials Worksheet
- Definition of Monomial
Example
Example 1
Let's multiply the following 2 monomials: (5x )(3x2y)
Step 1Group variables by exponent and group the coefficients (apply commutative property of multiplication)
(5 • 3)(x • x2)(y)
Multiply each like term (remember your exponents laws
(5 • 3)(x • x2)(y)=(15)( x(2+1))(y)
15x3y
Video Tutorial
on How To Multiply Monomials
Practice Problems
Group variables by exponent and group the coefficients (apply commutative property of multiplication)
(2 • 4)(x • x3)(k)
Multiply each like term (remember your exponents laws)
2 • 4)(x • x3)(k) = (8)( x(1 + 3))(k)
8x4k
Group variables by exponent and group the coefficients (apply commutative property of multiplication)
(5 • 7)(x2 • x5)(k4 • k)
Multiply each like term (remember the exponents rules)
(5 • 7)(x2 • x5)(k4 • k)
(35)( x(2 + 4))(k(4 + 1))
35 x6
Group variables by exponent and group the coefficients (apply commutative property of multiplication)
(6 • 2 • 5)(x4 • x3 • x2)(k8 • k)(z)
Multiply each like term (remember the exponents rules)
(6 • 2 • 5)(x4 • x3 • x2)(k8 • k)(z)
(60)( x(4 + 3 + 2))(k(8 + 1))(z)
60 x9k9 z
Group variables by exponent and group the coefficients (apply commutative property of multiplication)
( 7 • 3 • 9 )( a4 • a5 ) ( t7 • t3 • t5 )( k2 • k4 )(f)
Multiply each like term (remember the exponents rules)
( 7 • 3 • 9 )( a4 • a5 ) ( t7 • t3 • t5 )( k2 • k4 )(f)
(189)( a(4 + 5))(t(7 + 3 + 5 ))( k(2 + 4))( f)
189 a9 t15 k6f