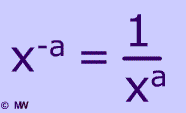There are many different laws of exponents. This page covers the 3 most frequently studied formulas in Algebra I. If you are looking for other laws, visit our exponents home page.
There are many different laws of exponents. This page covers the 3 most frequently studied laws of exponents (Rules 1-3 below).
Rule 1: $$ \boxed{ x^a \cdot x^ b = x^{a \red + b} } \\ \text{Example : } \\ 3^4 \cdot 3^2 = 3^{4+2} \\ 3^4 \cdot 3^2 = 3^{6} $$
Rule 2: $$ \boxed{ \frac{ x^a } { x^ b }= x^{a \red - b} } \\ \text{Example : } \\ \frac{ 7^6 } { 7^ 2 }= 7^{6 \red - 2} \\ = 7^4 $$
Rule 3: $$ \boxed{ (x^a)^ b = x^{a \red \cdot b} } \\ \text{Example : } \\ (3^2)^ 4 = 3^{2 \red \cdot 4} \\ = 3^{8} $$
Rule 4: $$ \boxed{ x^{- \red a} = \frac {1}{x^{\red a}} } $$
seperate lessonRule 5: $$ \boxed{ x^{\frac m n} = ? } $$
seperate lesson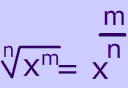
Be Careful
Every rule above only works when the bases are the same.
So, something like $$ \red 3 ^2 \cdot \red 5^3 $$ can not be simplified using these rules because the bases are different
Practice Problems
Problem 1
Since we are multiplying exponents we add the exponents:
$ x^3 \cdot x^2 = x^{3+2} = x^5 $
Problem 2
Use the power rule of exponents and multiply exponents:
$ (x^3) ^2 = x^{(3 \cdot 2)}= x^6 $
Problem 3
Use the quotient rule of exponents and subtract the exponents:
$ \frac {x^5}{ x^3} = x^{(5 - 3)}= x^2 $
Problem 4
Since we are multiplying exponents we add the exponents
$ x^{11} \cdot x^5 = x^{11+5} = x^{16} $
Problem 5
You cannot simplify this expression! Remember that all of the rules on this page only work when the exponents have the same base!
Exponent Rules Covered Elsewhere
Negative Exponents
Fraction Exponents
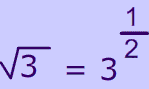
Fraction exponents are explained separately here