| ∠ A | |
|---|---|
| ∠ B | |
| ∠ C | |
| ∠ D |
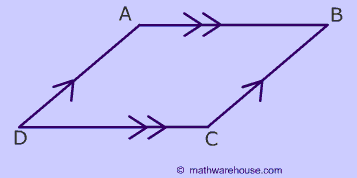
A parallelogram is a quadrilateral made from two pairs of intersecting parallel lines. There are several rules involving:
Interactive Parallelogram
Two Pairs of Parallel Lines
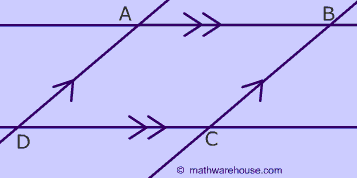
To create a parallelogram just think of 2 different pairs of parallel lines intersecting. ABCD is a parallelogram.

Angles of Parallelogram
Opposite Angles are Congruent
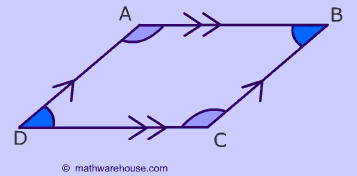
$$ \angle D \cong \angle B \\ \angle A \cong \angle C $$
Triangles can be used to prove this rule about the opposite angle.
Consecutive angles are supplementary
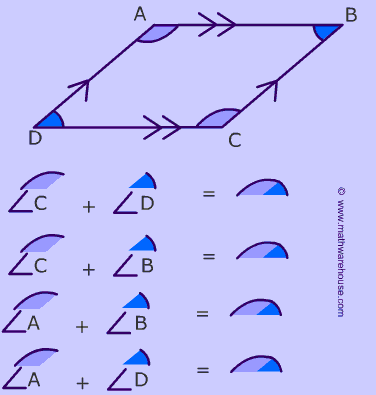
The following pairs of angles are supplementary
$$ \angle C $$ and $$ \angle D $$
$$ \angle C $$ and $$ \angle B $$
$$ \angle A $$ and $$ \angle B $$
$$ \angle A $$ and $$ \angle D $$
To explore these rules governing the angles of a parallelogram use Math Warehouse's interactive parallelogram.
Problem 1
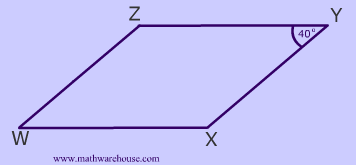
There are many different ways to solve this question. You know that the opposite angles are congruent and the adjacent angles are supplementary.
$$ \angle \red W = 40^{\circ} $$ since it is opposite $$ \angle Y $$ and opposite angles are congruent.
Since consecutive angles are supplementary
$$
m \angle Y + m \angle Z = 180 ^{\circ}
\\
40^{\circ} + m \angle Z = 180 ^{\circ}
\\
m \angle Z = 180 ^{\circ} - 40^{\circ}
\\
m \angle \red Z = 140 ^{\circ}
$$
Problem 2
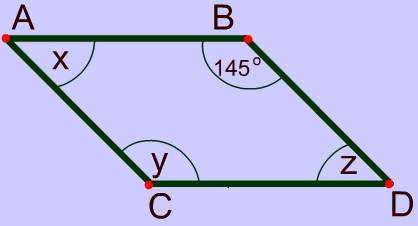
Sides of A Parallelogram
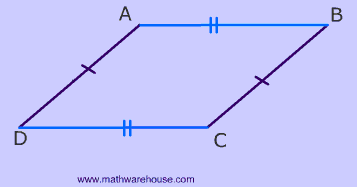
The opposite sides of a parallelogram are congruent.
Triangles can be used to prove this rule about the opposite sides.
To explore these rules governing the sides of a parallelogram use Math Warehouse's interactive parallelogram.
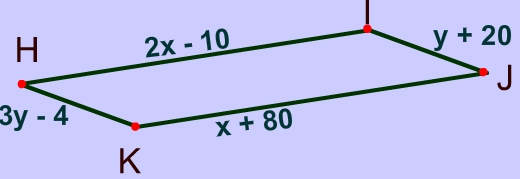
Problem 3
Problem 4
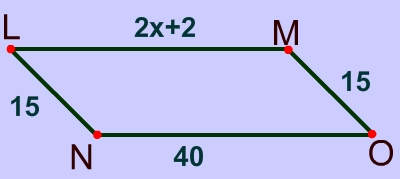
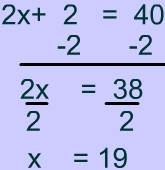
Problem 5
Since opposite sides are congruent you can set up the following equations and solve for $$x $$: $ \text{ Equation 1} \\ 2x − 10 = x + 80 \\ x - 10 = 80 \\ x = 90 $
Since opposite sides are congruent you can set up the following equations and solve for $$y $$: $ \text{ Equation 2} \\ 3y − 4 = y + 20 \\ 2y − 4 = 24 \\ 2y = 24 \\ y = 12 $
Diagonals
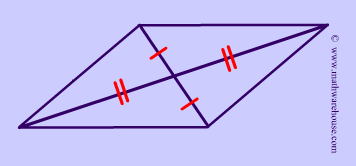
The diagonals of a parallelogram bisect each other.
AO = OD
CO = OB
To explore these rules governing the diagonals of a parallelogram use Math Warehouse's interactive parallelogram.
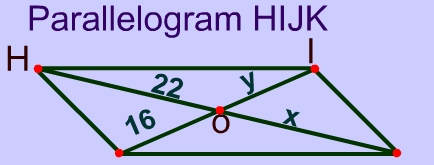
Problem 6
Since the diagonals bisect each other, y = 16 and x = 22
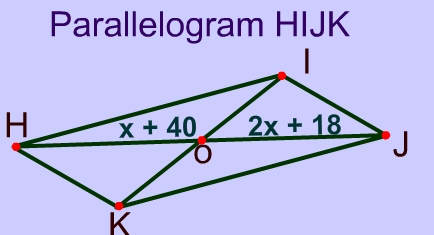
Problem 7
$$ x + 40 = 2x + 18 \\ 40 = x +18 \\ 40 = x + 18 \\ 22 = x $$
A classic activity: have the students construct a quadrilateral and its midpoints, then create an inscribed quadrilateral. Then ask the students to measure the angles, sides etc.. of inscribed shape and use the measurements to classify the shape (parallelogram). Designed with Geometer's Sketchpad in mind .