Graph and Formula for the Unit Circle as a function of Sine and Cosine

Graph of Cotangent from Unit circle

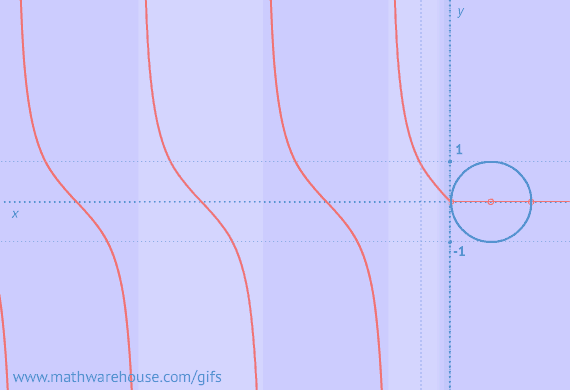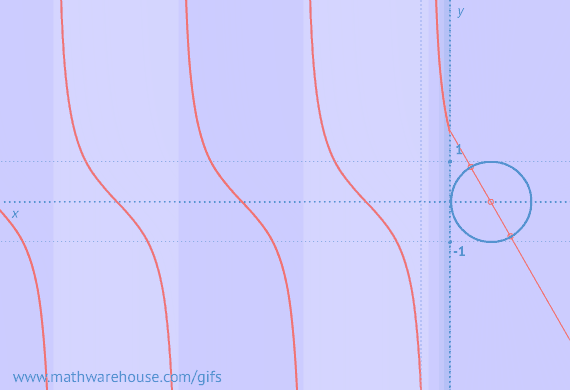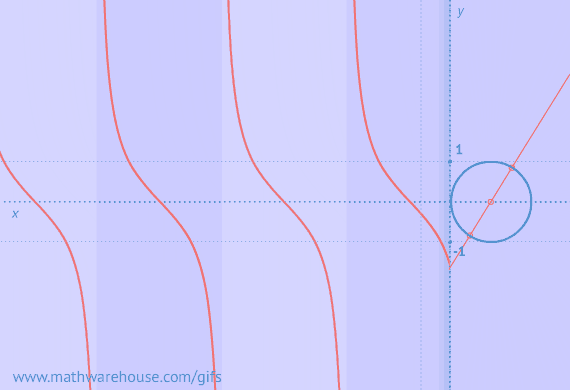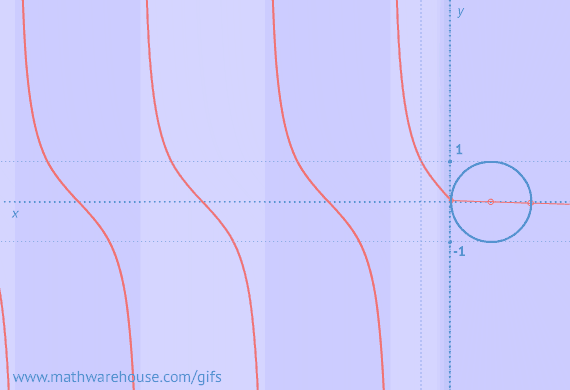
Graphs of Sine/Cosine From Unit Circlle

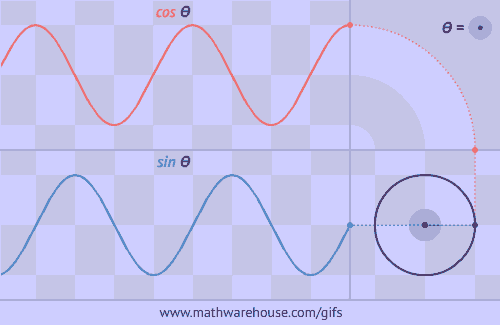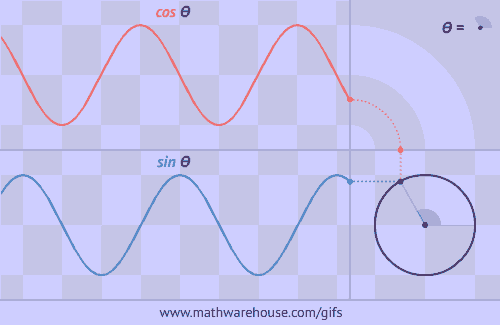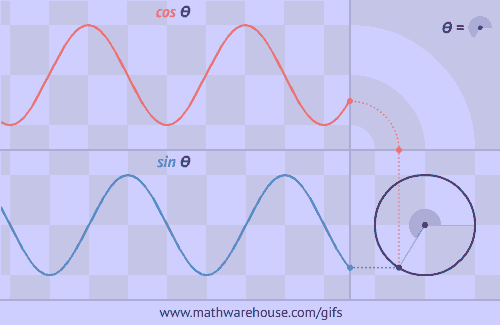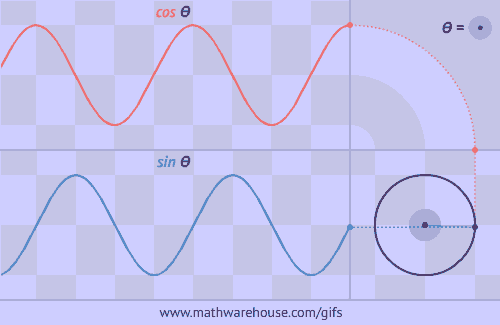
The Unit Circle is a circle with a radius of 1. The angle that we rotate the radius uses the greek letter θ.

Formula for the Unit Circle

The formula for the unit circle relates the coordinates of any point on the unit circle to sine and cosine. According to the formula, the x coordinate of a point on the unit circle is $$cos (\theta)$$ and the y coordinate of a point on the unit circle is $$ sin(\theta)$$ where Θ represents the measure of an angle that goes counter clockwise from the positive x-axis. This formula is much easier to see and understand from a picture. See the first problem below.

Demonstration of Unit Circle's Formula

Practice Problems

Problem 1

Can you fill in the entire unit circle?

Filled in Unit Circle, unit circle printable

Problem 2

Picture of the unit circle.

The first lesson to learn about the unit circle is what should replace the red questions marks below. In other words, what is the x and the y coordinates of any point on the unit circle.

The value of the x coordinate is the $$ cos(\theta)$$ and the y coordinate is $$ sin(\theta)$$.

Problem 3

Identifying Cosine, Sine and Tangent lines in the Unit Circle.

The circle below has a radius of 1.
Which line segment represent

$$ sin(\theta)$$
$$ cos(\theta)$$
$$ tan(\theta)$$

Remember the formula for the unit circle. Cosine represents the x value, segment AB, sine represents the y value or CB and the tangent line rests outside the circle and is DF.

Problem 4

The circle below has a radius of 1.
Which line segment represent

$$ sin(\theta)$$
$$ cos (\theta)$$
$$ tan(\theta)$$

Remember the formula for the unit circle. Cosine represents the x value, segment AB, sine represents the y value or CB and the tangent line rests outside the circle and is DF.

Problem 5

Use the formula for the unit circle to identify which line segments represent.

$$ sin(\theta)$$
$$ cos (\theta)$$
$$ tan(\theta)$$

Remember the formula for the unit circle. Cosine represents the x value, segment PL, sine represents the y value or PO and the tangent line rests outside the circle and is NM.

Problem 6

Use the unit circle formula to identify which segment represent.

$$ sin(\theta)$$
$$ cos (\theta)$$
$$ tan(\theta)$$

Remember the formula for the unit circle. Cosine represents the x value, segment AE, sine represents the y value or ED and the tangent line rests outside the circle and is BC.

Problem 7

Use the unit circle formula to identify which segment represents.

$$ sin(\theta)$$
$$ cos (\theta)$$
$$ tan(\theta)$$

Remember the formula for the unit circle. Cosine represents the x value, segment OS, sine represents the y value or SQ and the tangent line rests outside the circle and is PR.