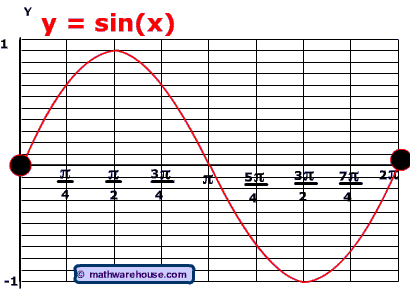
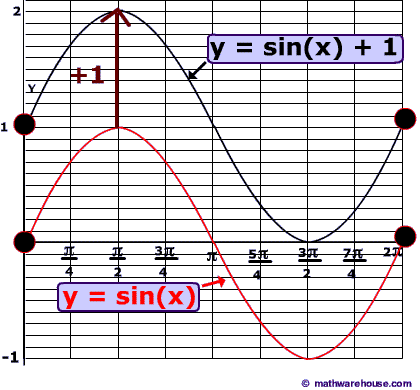
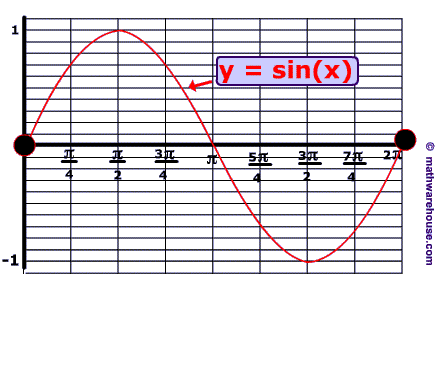
Translation and phase shifts of sine and cosine graphs. How equation relates to graph. Illustrated demonstrations and examples

A translation is a type of transformation that is isometric (isometric means that the shape is not distorted in any way). A translation of a graph, whether its sine or cosine or anything, can be thought of a 'slide'. To translate a graph, all that you have to do is shift or slide the entire graph to a different place.

Vertical Translations of Sine and Cosine graphs

Example

If you're on this web page, you should be very familiar with the graph of y =sin(x) as shown below $$ 0 \le x \le 2 \pi $$. An example of first type of translation that we wil look at is y = sin(x) + 1.

Below you can see both the original graph of y =sin(x) and the graph of the translation y = sin(x) + 1.

translation of the graph of sinx downward by one

Problem 1

Based on the example above you can figure out, what the graph of the following translation would look like y = sin(x) − 1.

This translation expresses a vertical shift downwards by 1.

Problem 2

What would the graph of the following equation look like: $$ \frac{1}{2} sin(2x) - \frac{1}{2} $$ ?
(Note this question assumes that you have studied amplitude of sine equations as well as period of sine and cosine graphs).

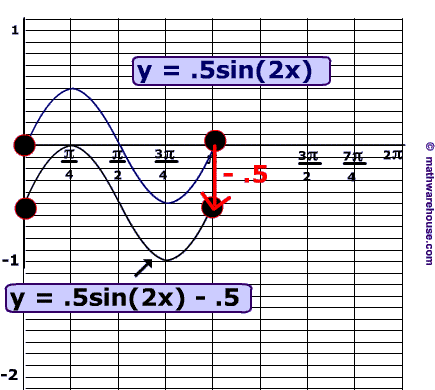
Problem 3

What would be the graph of the function $$g(x)=\sin (-x)$$ comparing to the graph of $$f(x)=\sin (x)$$?

Graph of f(x) = sin (-x) is the reflection of the graph of f(x) = sin (x) about x-axis.

Each pair of corresponding points on the graphs has the same distance form the x-axis.

For example, points A and B are two corresponding points on the graphs, and they are at the same distance from the x-axis. That is, AM = BM.

Problem 4

What would be the graph of the function $$g(x)=\sin \left(x+\frac{5\pi}{4} \right)$$ comparing to the graph of $$f(x)=\sin \left(x+\frac{\pi}{4} \right)$$?

The difference between the variables of the two functions is:

                                        $$\left(x+\frac{5\pi}{4} \right)-\left(x+\frac{\pi}{4} \right)$$
                                    
                                        = $$x+\frac{5\pi}{4} -x-\frac{\pi}{4}$$
                                    
                                        = $$\frac{5\pi}{4} -\frac{\pi}{4}$$
                                    
                                        = $$\frac{4\pi}{4}$$
                                    
                                        = $$\pi$$

So, the graph of f(x) is transferred $$\pi $$ units to the left to create the graph of g(x).

Problem 5

How graph of the function $$f(x)=\sin \left(3x-\frac{\pi}{3} \right)$$ is transferred to graph of $$g(x)=\sin \left(3x+\frac{\pi}{3} \right)$$?

The difference between the variables of the two functions is:

                                    $$\left(3x+\frac{\pi}{3} \right)-\left(3x-\frac{\pi}{3} \right)$$
                                    
                                        = $$3x+\frac{\pi}{3} -3x+\frac{\pi}{3}$$
                                    
                                        = $$\frac{\pi}{3} +\frac{\pi}{3}$$
                                    
                                        = $$\frac{2\pi}{3}$$

Therefore, the graph of f(x) is transferred $$\frac{2\pi}{3} $$ units to the left to generate the graph of g (x)

Problem 6

What would be the graph of the function $$g(x)=\sin (-x)-3$$ comparing to the graph of $$f(x)=\sin (-x)$$?

Difference between the values of f(x) and g(x) is -3. Therefore, g(x) is obtained by moving f(x) 2 units downward.

Problem 7

How would the graph of the function $$f(x)=\sin (x)$$ be transferred to the graph of $$g(x)=\sin (x+2)+2$$?

First graph of $$f(x)=\sin (x)$$ is transferred to the graph of $$h(x)=\sin (x+2)$$ by moving 2 units to the left as shown in the graph below.

Then the graph of g(x) is obtained by moving the graph of h(x) upward 2 units.

Problem 8

What would be the graph of the function $$f(x)=\cos (-x)$$ comparing to the graph of $$g(x)=-\cos (x)$$?

Graph of cos (-x) is exactly the same as the graph of cos (x).

So, g(x) is exactly the reflection of f(x) about x-axis.

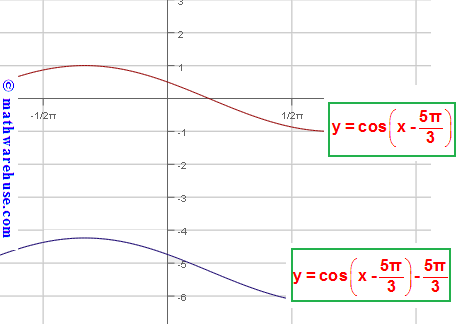
Problem 9

How the graph of the function $$f(x)=\cos \left(x-\frac{5\pi}{3} \right)$$ is transferred to the graph of $$g(x)=\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} $$?

                                        $$g(x)-f(x)=\left[\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} \right] - \cos \left(x-\frac{5\pi}{3} \right)$$
                                    
                                        = $$\cos \left(x-\frac{5\pi}{3} \right)-\frac{5\pi}{3} -\cos \left(x-\frac{5\pi}{3} \right)$$
                                    
                                        = $$-\frac{5\pi}{3} $$

So, the graph of f(x) is moved $$\frac{5\pi}{3} $$ units downward to generate the graph of g(x).

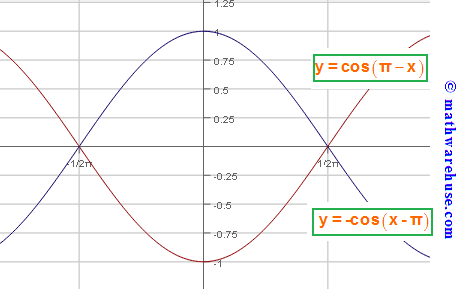
Problem 10

What would be the graph of the function $$g(x)=-\cos \left(x-\pi \right)$$ comparing to the graph of $$f(x)=\cos \left(\pi -x\right)$$?

$$f(x)=\cos \left(\pi -x\right)$$ is the same as $$f(x)=\cos \left(x-\pi \right)$$. So $$g(x)=-\cos \left(x-\pi \right)$$ is the reflection of f(x) about x-axis.

Problem 11

How would the graph of the function $$f(x)=\cos \left(x-\frac{\pi}{3} \right)$$ is transferred to the graph of $$g(x)=\cos \left(\frac{\pi}{3} \, \, -\, \, x\right)\, \, -\, \, \frac{\pi}{3} $$?

$$g(x)=\cos \left(\frac{\pi}{3} \, \, -\, \, x\right)\, \, -\, \, \frac{\pi}{3} $$ is the same as $$g(x)=\cos \left(x-\frac{\pi}{3} \, \, \right)\, \, -\, \, \frac{\pi}{3} $$.
So, f(x) is moved downward $$\frac{\pi}{3} $$ units.

Problem 12

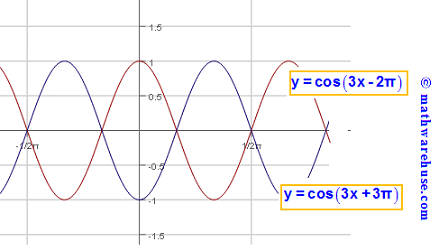
What would be the graph of the function $$g(x)=\cos (3x+3\pi)$$ comparing to the graph of $$f(x)=\cos (3x-2\pi)$$?

                                        $$(3x+3\pi)-(3x-2\pi)$$
                                    
                                        = $$3x+2\pi -3x+3\pi$$
                                    
                                        = $$2\pi +3\pi$$
                                    
                                        = $$5\pi$$

So, the graph of f(x) moved $$5\pi $$ units to the left in order to generate the graph of g(x).