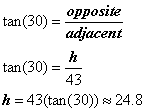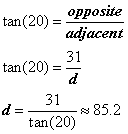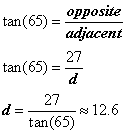Example 1
What is the height of the tree below?
$ tan(16) = \frac{opp}{adj} \\ tan(16) = \frac{14}{\red x} \\ \red x = \frac{14}{tan(16)} \\ \red x = 48.8 $
problem 1
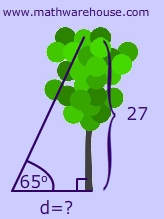
At 57" from the base of a building you need to look up at 55° to see the top of a building. What is the height of the building?
$ tan(55) = \frac{opp}{adj} \\ tan(55)= \frac{\red x }{ 57} \\ \red x = 57 \cdot tan(55) \\ \red x = 81.4 $
Problem 2
Step 1
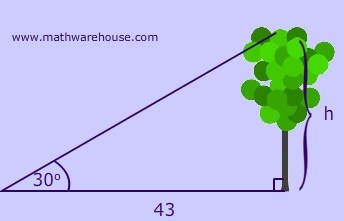
First, you should draw and label a picture of this word problem.
Step 2
![real world sohcahtoa]()
The illustration:
Rest of Steps
![tree height]()
Now, set up your trig ratio and solve for a side length:
Problem 3
Step 1
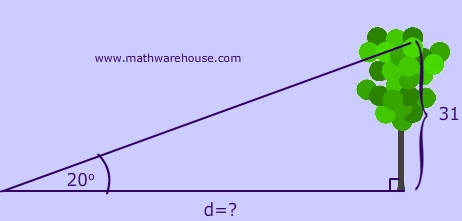
First, you should draw and label a picture of this word problem.
Step 2
![find height of the tree]()
The illustration:
Rest of Steps
![tree height]()
Now, set up the tangent ratio and solve for a side length:
Problem 4
Step 1
First, you should draw and label a picture of this word problem.
Step 2
![find distance to tree]()
The illustration:
Rest of Steps
![answer]()
Now, set up your trig ratio and solve for a side length:
