The Formula
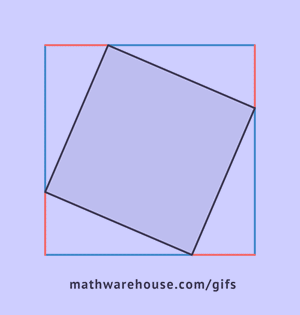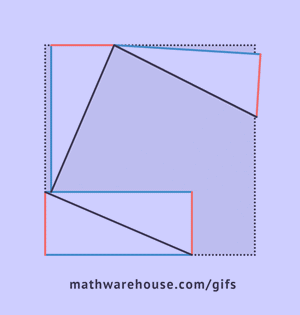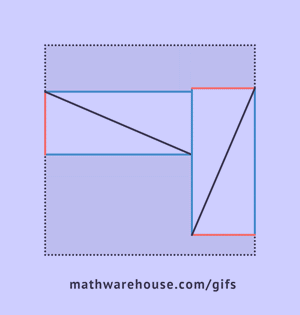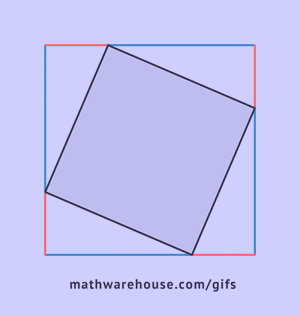
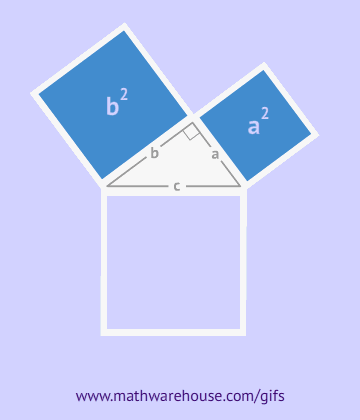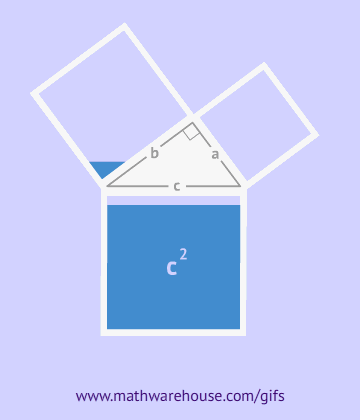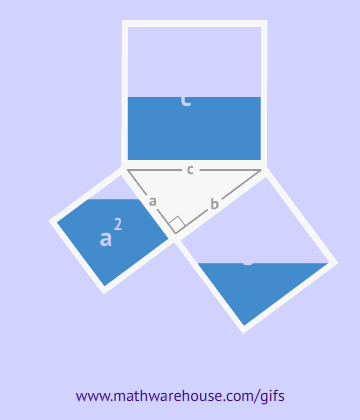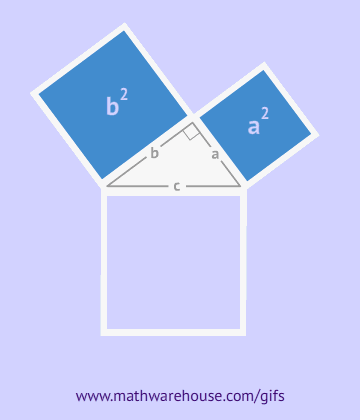
The picture below shows the formula for the Pythagorean theorem. For the purposes of the formula, side $$ \overline{c}$$ is always the hypotenuse. Remember that this formula only applies to right triangles.

How to Use The Pythagorean Theorem
The picture below shows the formula for the Pythagorean theorem. For the purposes of the formula, side $$ \overline{c}$$ is always the hypotenuse. Remember that this formula only applies to right triangles.
When you use the Pythagorean theorem, just remember that the hypotenuse is always 'C' in the formula above. Look at the following examples to see pictures of the formula.
More on the Pythagorean theorem
More on the Pythagorean theorem
on How to Use the Pythagorean Theorem
of Using the Pythagorean Theorem
Use the Pythagorean theorem to determine the length of X.
Identify the legs and the hypotenuse of the right triangle.
The legs have length 6 and 8. $$X $$ is the hypotenuse because it is opposite the right angle.
Substitute values into the formula (remember 'C' is the hypotenuse).
$ A^2+ B^2= \red C^2 \\ 6^2+ 8^2= \red X^2 $
$A^2+ B^2= \red X^2 \\ 100= \red X^2 \\ \sqrt {100} = \red X \\ 10= \red X $
Use the Pythagorean theorem to determine the length of X.
Identify the legs and the hypotenuse of the right triangle.
The legs have length 24 and $$X$$ are the legs. The hypotenuse is 26.
Substitute values into the formula (remember 'C' is the hypotenuse).
$ \red A^2+ B^2= C^2 \\ \red x^2 + 24^2= {26}^2 $
$ \red x^2 + 24^2= 26^2 \\ \red x^2 + 576= 676 \\ \red x^2 = 676 - 576 \\ \red x^2 = 100 \\ \red x = \sqrt { 100} \\ \red x = 10 $
Remember our steps for how to use this theorem. This problems is like example 1 because we are solving for the hypotenuse .
Step 1Identify the legs and the hypotenuse of the right triangle.
The legs have length 14 and 48. The hypotenuse is X.
Substitute values into the formula (remember 'C' is the hypotenuse).
$ A^2 + B^2 = C^2 \\ 14^2 + 48^2 = x^2 $
Solve for the unknown.
$ 14^2 + 48^2 = x^2 \\ 196 + 2304 = x^2 \\ \sqrt{2500} = x \\ \boxed{ 50 = x} $
Identify the legs and the hypotenuse of the right triangle.
The legs have length 9 and X. The hypotenuse is 10.
Substitute values into the formula (remember 'C' is the hypotenuse).
$ A^2 + B^2 = C^2 \\ 9^2 + x^2 = 10^2 $
Solve for the unknown.
$ 9^2 + x^2 = 10^2 \\ 81 + x^2 = 100 \\ x^2 = 100 - 81 \\ x^2 = 19 \\ x = \sqrt{19} \approx 4.4 $
Identify the legs and the hypotenuse of the right triangle.
The legs have length '10' and 'X'. The hypotenuse is 20.
Substitute values into the formula (remember 'C' is the hypotenuse).
$ A^2 + B^2 = C^2 \\ 10^2 + \red x^2 = 20^2 $
Solve for the unknown.
$ 10^2 + \red x^2 = 20^2 \\ 100 + \red x^2 = 400 \\ \red x^2 = 400 -100 \\ \red x^2 = 300 \\ \red x = \sqrt{300} \approx 17.32 $


 Step 1
Step 1
 Step 1
Step 1