Definition
of the Centroid of a Triangle
The Centroid is a point of concurrency of the triangle. It is the point where all 3 medians intersect and is often described as the triangle's center of gravity or as the barycent.
Properties of the Centroid- It is formed by the intersection of the medians.
- It is one of the points of concurrency of a triangle.
- It is always located inside the triangle (like the incenter, another one of the triangle's concurrent points)
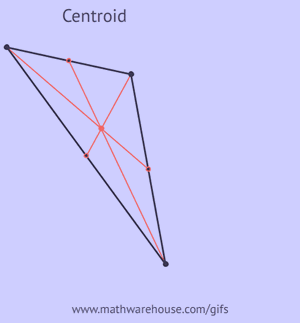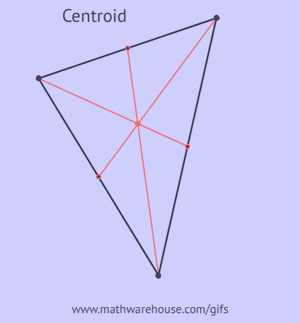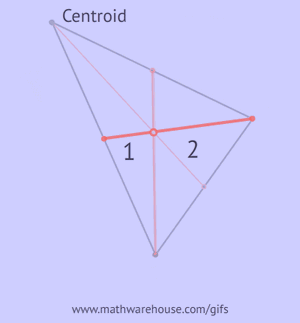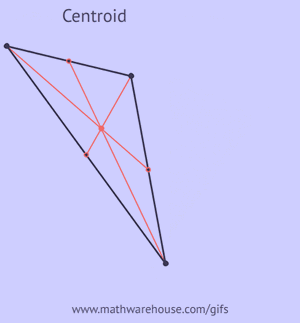
- The centroid divides each median in a ratio of 2:1. In other words, the centroid will always be 2/3 of the way along any given median. See bottom set of pictures.
Picture of Centroid of an Acute Triangle ![Picture of Centoid of a Triangle]()
Picture of Centroid of an Obtuse Triangle ![Centroid of Obtuse Triangle]()
Pictures of the 2:1 ratios formed by centroid and medians
Practice Problems
Problem 1
Point A is a midpoint and Point B is the centroid of the triangle pictured below, if the length of BC is 12, what is the length of AB ? You may assume the picture is drawn to scale.
Problem 1
Point A is a midpoint and Point B is the centroid of the triangle pictured below, if the length of AB is 7, what is the length of BC ? You may assume the picture is drawn to scale.
-
Related Links:
- Triangles
- Triangle Types
- Interactive Triangle
- images
- Free Triangle Worksheets
