Practice Problems
Problem 1
~
Problem 2
CA and YW are corresponding.
Follow the letters: $$ \triangle \red A B \red C$$ ~ $$\triangle \red W X \red Y$$
For more practice identifying corresponding sides and angles, go here.
Problem 3
| Step 1) Pick a pair of corresponding sides (follow the letters) |
AB and AD are corresponding based on the letters of the triangle names
$$ \triangle \color{red}{AB}C$$ ~ $$\triangle \color{red}{AD}E$$ |
| Step 2) Substitute side lengths into proportion | $$ \frac{AB}{AD} = \frac{40}{30} $$ |
| Step 3) Simplify (if necessary) |
$$ \frac{40}{30}=\frac{4}{3} $$ |
Problem 4
If If $$ \triangle $$ ACB ~ $$\triangle $$AXY and the similarity ratio is 2:5, what ist the measure of sie AC?
Since AX and AC are corresponding, just set up a proportion and solve:
$ \frac{2}{5} = \frac{x}{10} \\ \frac{2 \cdot 10}{5} = x \\ x = 4 $
For more problems like this, go here.
Problem 5
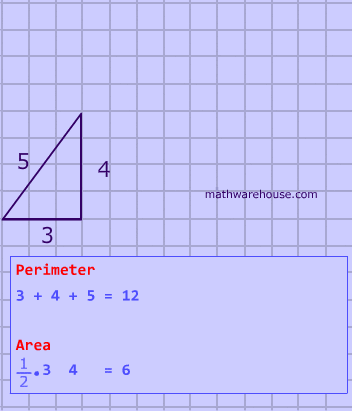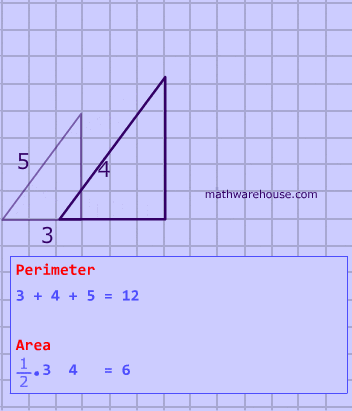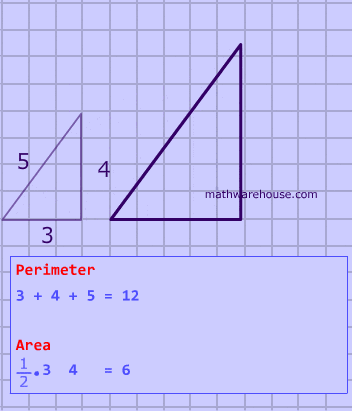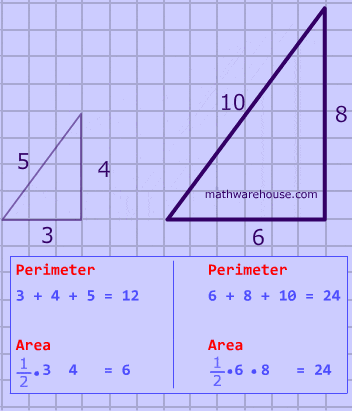
Two triangles are similar, and the ratio of each pair of corresponding sides is 4 : 3 . Which statement regarding the two triangles is true?
Problem 6
Two triangles are similar, and the ratio of each pair of corresponding sides is 2 : 5. Which statement regarding the two triangles is true?
Problem 7
$ \frac{P}{G} = \frac{H}{b} \\ \frac{4}{12} = \frac{3}{b} \\ 4 \cdot b = 36 \\ b= 9 $
For more problems like this, go here.
Problem 8
Are the two triangles below similar?
No, because the ratios of the sides are not proportional
For more problems like this, go here.
Problem 9
Are the two triangles below similar?
No, because the ratios of the sides are not proportional.
For more problems like this, go here.
Problem 10
