Radioactive Half Life

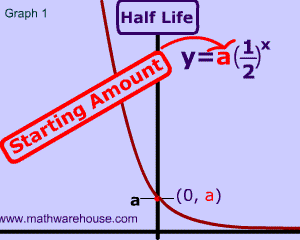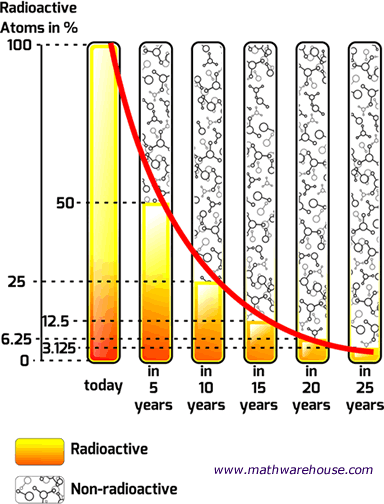
In this first chart, we have a radioactive substance with a half life of 5 years. As you can see, the substance initially has 100% of its atoms, but after its first half life (5 years) only 50% of the radioactive atoms are left.

That's what 'half life' means. Literally, half of the substance is gone every five years (the half life of this particular substance).

So, in our example , after the second life is over (that's 10 years since each half life is 5 years), there will be $$\frac 1 2$$ of $$ 50\% $$ of the substance left, which, of course is $$ 25 \% $$.

And the pattern continues, every 5 years another half life reduces the substance by $$ \frac 1 2 $$, so after the the third life is over ( the 15 year mark), there will be $$\frac 1 2 $$ of $$ 25\% $$ of the substance left , which is $$ 12.5 \% $$.

As you can might be able to tell from Graph 1,Half life is a particular case of exponential decay. One in which 'b' is $$ \frac 1 2 $$.

So, generally speaking, half life has all of the properties of exponential decay.

The coefficient 'a', represents the starting amount.

As you can see from Graph 2, the larger the coefficient the greater the 'starting amount'. Conversely, the smaller coefficients lead to smaller/lower 'starting amounts'.

Typically, we do not even consider the negative x values because the x-axis typically represents time.