Quick Summary
- When working with graphs, the best we can do is estimate the value of limits.
- If the one-sided limits seem to be equal, we use their value as the value of the limit.
Examples
Example 1
Use the graph to estimate $$\displaystyle\lim\limits_{x\to4} f(x)$$

Examine the limit from the left.

Examine the limit from the right.

The one-sided limits are the same, so the limit exists.
Answer: $$\displaystyle\lim\limits_{x\to4} f(x) \approx 5$$
Example 2
Use the graph to estimate $$\displaystyle\lim\limits_{x\to-3} f(x)$$

Examine the limit from the left.

Examine the limit from the right.

The one-sided limits are the same, so the limit exists.
Answer: $$\displaystyle\lim\limits_{x\to-3}f(x) \approx 2$$
Example 3
Use the graph to evaluate $$\displaystyle\lim\limits_{x\to0} f(x)$$

Examine the limit from the left and from the right.
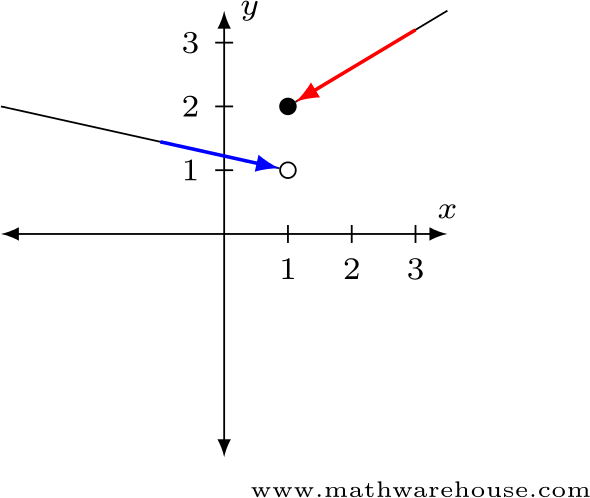
Examine the one-sided limits.
The limit from the left is not the same as the limit from the right. 
Answer: The limit does not exist.
Practice Problems
Use the graph below to estimate the value of the limits in questions 1--5.


Answer: $$\displaystyle\lim\limits_{x\to-3} f(x) \approx 4$$

Answer: $$\displaystyle\lim\limits_{x\to-2} f(x)$$ does not exist.

Answer: $$\displaystyle\lim\limits_{x\to0} f(x) \approx 0$$

Answer: $$\displaystyle\lim\limits_{x\to2} f(x) \approx 1$$

The limit from the right doesn't exist.
Answer: $$\displaystyle\lim\limits_{x\to4} f(x)$$ does not exist.