What kind of notation ?
| Notation | Meaning |
| $$ g \cdot f (x)$$ | "g of f of x" |
| $$ g ( f (x) ) $$ | "g of f of x" |
| Notation | Meaning |
| $$ g \cdot f (x)$$ | "g of f of x" |
| $$ g ( f (x) ) $$ | "g of f of x" |
A composition involves 2 (or more) functions. In a composition, you use the output of one function as the input of a second function.
In the following flow chart,
The
output of $$ f(x) $$
is used as the input of our second function $$ g(x)) $$
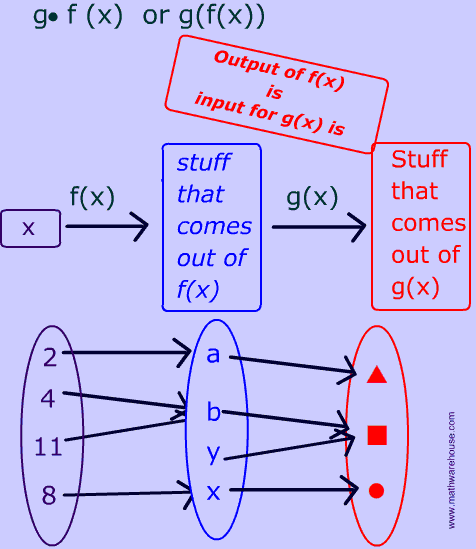
As you can see the range of f(x) is the domain of g(x) .
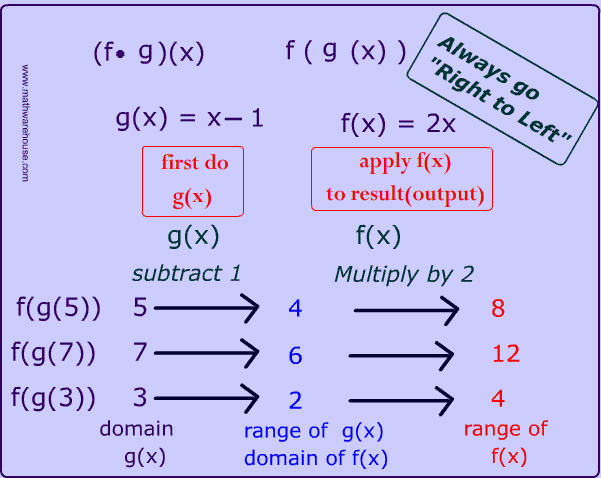
We have 2 functions that we will use for our composition:
$ f(x) = 2x $
$ g(x) = x- 1 $
The flow chart below shows a step by step walk through of $$ (f \cdot g)(x) $$.
Perform right side function $$ g(x)$$ .
Apply the left side function $$ f(x) $$
to the output of Step 1 .
Does $$ f(g(x)) = g(f (x)) $$?
Remember that the commutative property states that "order does not matter". ( link )
Multiplication is commutative because $$ 3 \cdot 2 = 2 \cdot 3 $$.
On the other hand, subtraction is not commutative because $$ 3 - 2 \ne 2 - 3 $$.
In other words, does it make if difference whether we write $$ f(g(x)) $$ vs $$ g(f(x))$$ ?
To answer that question, let's explore a specific example:
$$ \red{ f(x) = x + 5} $$
$$ \blue{ g(x) = 4x} $$
Let's evaluate $$ \red {f}(\blue{g}(3)) $$ and $$ \blue{g}(\red {f}(3)) $$ and see if we get the same answer.
$$ \red {f}(\blue{g}(3)) $$
$$ \red {f}(\blue{g}(3)) \\ \blue{g}(3) =4 \cdot 3 = 12 \\ \red {f}(12) = 12 + 5 \\ \red {f}(12) = \boxed {17 } $$
$$ \blue{g}(\red {f}(3)) $$
$$ \blue{g}(\red {f}(3)) \\ \red {f}(3) = 3+ 5 = 8 \\ \blue{g}(8) = 4 \cdot 8 \\ \blue{g}(8) = \boxed {32 } $$
Composition of functions are not commutative because $$ f(g(3)) \red { \ne} g(f(3)) $$.
In other words, what if $$f(x)$$ and $$ g(x)$$ are inverses?
Again, the best way to understand this is to try some examples, and see what happens.
Let $$ \bf{ \red { f(x) = x + 3}} \\ \bf{ \blue{ g(x) = f^{-1}(x) = x -3}} $$
What is $$ f(g(x)) = ? $$
$$ \red {f(}\blue{g(x)} \red {)} \\ = \red {f(}\blue{ x-3} \red {)} \\ = \red {(}\blue{ x-3} \red {) +3}= \bf{ x} $$
Let $$ \bf{ \red { f(x) = x^2}} \\ \bf{ \blue{ g(x) = f^{-1}(x) = \sqrt{x}}} $$
What is $$ f(g(x)) = ? $$
$$ \red {f(}\blue{g(x)} \red {)} \\ =\red {f(}\blue{ \sqrt{x}} \red {)} \\ = \red {(} \blue{ \sqrt{x}} \red {)^2} = \bf{ x} $$
Composition of inverse functions always evaluate to $$ x $$ (ie the input itself) .
$$ f(f^{-1}(x)) = \bf {x} $$
Therefore, you know that:$$ g(g^{-1}(5)) = 5 \\ a(a^{-1}(232232)) = 232232 \\ k(k^{-1}(-90210)) = -90210 \\ k(k ^{-1}(\bigstar)) = \bigstar \\ f(f^{-1}(stuff)) = stuff $$
If you think of the inverse function as 'undoing' the original function, this rule might make sense. Read more about inverse functions here.
Directions: Evaluate each composition of functions listed below.
Evaluate function $$ f(\red {g(2) }) $$.
Substitute that value into left side function $$ \red {f}(g(2)) $$.
Evaluate function $$ f(\red {g(8) }) $$.
Substitute that value into left side function $$ \red {f}(g(8)) $$.
Evaluate function $$ f(\red {h(18) }) $$.
Substitute that value into left side function $$ \red {f}(h(18)) $$.
Evaluate function $$ f(\red {b(5) }) $$.
Substitute that value into left side function $$ \red {f}(b(5)) $$.
Evaluate function $$ f(\red {m(11) }) $$.
Substitute that value into left side function $$ \red {f}(m(11)) $$.
Did you notice that the input of '11' is the same as the output for this composition.
Because these two functions are inverses of each other!
Remember that the rule about the composition of inverse functions.
Advanced problems - solving algebraically.
Substitute right side function into left side.
$$ \red { k(} \blue{ h(x) } \red {)} = \red { k(} \blue{ x + 3 } \red {)} \\ \red { k(} \blue{ x + 3 } \red {)} = \red {(} \blue{ x + 3 } \red {)^2 + (}\blue{ x + 3 } \red {)} $$
Simplify.
$$ \red {(}x^2 + 6x + 9 \red {) + (} x + 3 \red {)} \\ x^2 + 6x + 9 + x + 3 \\ x^2 + 7x + 12 $$
Substitute right side function into left side.
$$ \red { g(} \blue{ h(x) } \red {)} = \red { g(} \blue{ x + 4 } \red {)} \\ \red { g(} \blue{ x + 4 } \red {)} = \red {2(} \blue{ x + 4 } \red {)^2 - 3(}\blue{ x + 4 } \red {)} $$
Simplify.
$$ \red {2(} \blue{ x + 4 } \red {)^2 - 3(}\blue{ x + 4 } \red {)} \\ 2 (x^2 + 8x + 16) - 3 \cdot x - 3 \cdot 4 \\ 2x^2 + 2\cdot 8x + 2\cdot 16 - 3 x - 12 \\ 2x^2 + 16x + 32 - 3x - 12 \\ 2x^2 + 13x +20 $$