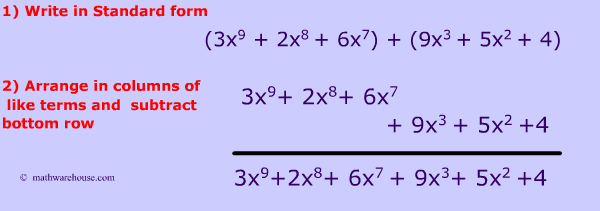Whether you want to add polynomials or subtract them, you follow a similar set of steps.
General Steps
Arrange the Polynomial in standard form.
Standard form of a polynomial just means that the term with highest degree is first and each of the following terms.
Step 2Arrange the like terms in columns and add the like terms.
Example 1
Let's find the sum of the following two polynomials.
$$ (3y^5 - 2y + y^4 + 2y^3 + 5)$$ and $$(2y^5 + 3y^3 + 2 + 7)$$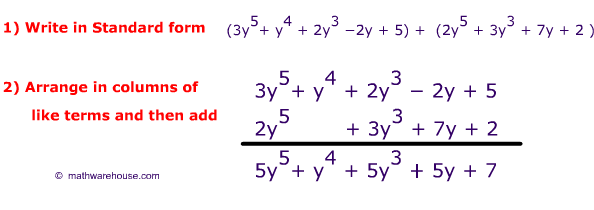
Subtracting Polynomials
Example 2
Let's find the difference of the same two polynomials.
$$ (3y^5 - 2y + y^4 + 2y^3 + 5)$$ and $$(2y^5 + 3y^3 + 2 + 7)$$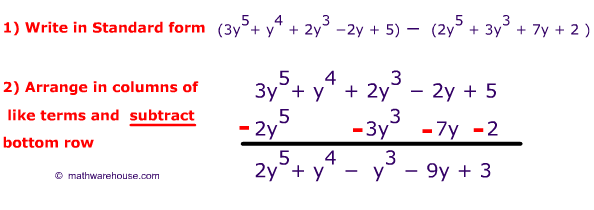
Practice Problems
Problem 1
This problem is like example 1.
First, remember to rewrite each polynomial in standard form, line up the columns and add the like terms.
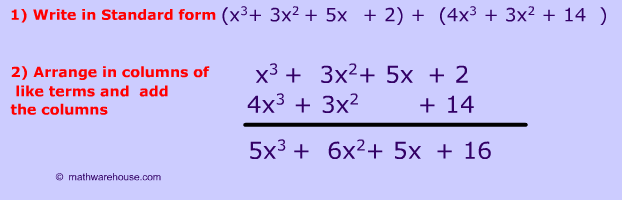
Problem 2
This problem is like example 1.
First, remember to rewrite each polynomial in standard form, line up the columns and add the like terms.
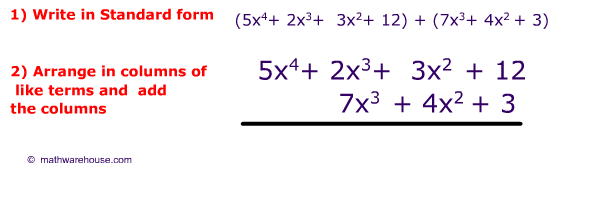
Problem 3
This problem is like example 2 since we are subtracting.
First, remember to rewrite each polynomial in standard form, line up the columns and add the like terms.
(Be careful with $$-11x^3$$ term; it is already negative, so subtracting a negative leads to a positive $$11x^3 $$)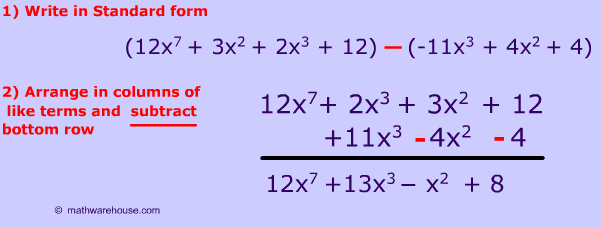
Problem 4
Although this problem involves addition, there are no like terms. If you line up the polynomials in columns, you will see that no terms are in the same columns.