Slope Intercept to Standard Form

How to convert from y = mx + b to Ax + By = C

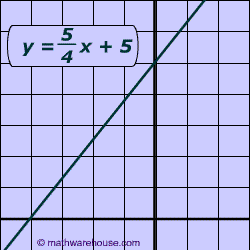
It is a common to ask to have to convert equation of line from slope intercept to standard form, as demonstrated by the pictures below.

General Formula Slope Intercept Form

Example of Converting from Slope Intercept to Standard Form

Example

Convert $$ y = \frac 5 4 x + 5 $$, graphed on the right, to standard form.

Diagram of slope intercept form of line
Step 1

Multiply by the least common denominator of the fractions (if any)

The only fraction is $$ \frac { 5}{ \red 4} $$ so you can multiply everything by 4.
$ \red 4 \cdot y = \red 4 \cdot \big( \frac { 5}{ \red 4}x +5 \big) \\ 4y = 5x + 20 $

Step 2

Move" y1 to the other side by adding its opposite to both sides of the equation and simplify

Solve for the y-intercept (or "b" in the slope intercept equation) which is 20 in this example.

- begin calculator html -->

Use our Calculator

You can use the calculator below to find the equation of a line from any two points. Just type numbers into the boxes below and the calculator (which has its own page here) will automatically calculate the equation of line in standard and slope intercept forms

(x1,y1) ,
(x2,y2) ,
Clear
Toggle Points
loading and calculating...

Answer:
$ $

( Try this 'equation from 2 points' calculator on its own page here . )

Clear
Toggle Points

Practice Problems

Problem 1

Convert the the equation below from slope intercept form to standard form $$ y = \frac 2 3 x -4 $$

Step 1

Multiply by the least common denominator of the fractions

The only fraction is $$ \frac{2}{\red 3 } $$ so you can multiply everything by 3.

$$ \red 3 \cdot y = \red 3 \big( \frac{2}{\red 3 } -4 \big) \\ 3y = 2x-12 $$

Step 2

Solve for the y-intercept (or "b" in the slope intercept equation) which is 12 in this problem.

Problem 2

Change the the equation below from slope intercept to standard from $$ y = \frac 1 2 x + 5 $$

Step 1

Multiply by the least common denominator of the fractions (if any)

The only fraction is $$ \frac{1}{\red 2}$$ so you can multiply everything by 2.

$$ \red 2 \cdot y =\red 2 \cdot \big( \frac{1}{\red 2} x + 5 \big) \\2y = x + 10 $$

Step 2

Solve for the y-intercept (or "b" in the slope intercept equation) which is 10 in this problem.

Problem 3

Convert the the equation below from slope intercept to standard from $$ y = \frac 2 3 x + \frac 5 9 $$

Step 1

Multiply all terms by the least common denominator of the fractions

Unlike the prior examples, this problem has two fractions $$ \big( \frac 2 3 \text{ and } \frac 5 9 \big) $$ so you can multiply everything by their common denominator of $$ \red 9$$ .

$$ \red 9 \cdot y = \red 9 \big( \frac 2 3 x + \frac 5 9 \big) \\ 9y = 6x + 5 $$

Step 2

Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is 5.

Prroblem 4

Convert the the equation below from slope intercept to standard from $$ y = 5x + \frac 4 7 $$

Step 1

Multiply all terms by the least common denominator of the fractions

This problem only has the fraction $$ \frac{4}{\red 7 } $$ so we must multiply everything by 7.

$$ \red 7 \cdot y = \red 7 \big( 5x + \frac 4 7 \big) \\ 7y = 35x + 4 $$

Step 2

Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is 4.

Problem 5

Convert the the equation below from slope intercept to standard from (yes, this is a very challenging problem so let's see how sharp your algebra skills are.) $ y = ax + \frac b c $

Step 1

Multiply all terms by the least common denominator of the fractions

This problem only has the fraction $$ \frac{b}{ \red c } $$ so we must multiply everything by $$ \red c $$.

$$ \red c \cdot y = \red c \big( ax + \frac b c \big) \\ cy = cax + b $$ .

Step 2

Solve for the y-intercept (or "b" in the slope intercept equation) which, in this example, is the variable 'b'.

Ultimate Math Solver (Free)

Free Algebra Solver ... type anything in there!