Inverse Variation Formula and Graph. Animated Gif and Diagrams to illustrate formula, equation and graphical representation.

Quick Overview

The equation for inverse variation is written two different ways: $$ xy =k $$ or $$ y = \frac k x $$, where $$ k $$ is a constant.
$$ k $$ is called the constant of proportionality.
Inverse variation problems often contain one of the phrases: "varies inversely", "inversely proportional", "varies indirectly", or "indirectly proportional".
The graph of the inverse variation function is not linear. It is, instead, a hyperbola.
Not all inverse variation involve linear variables (see Example 5).

Basic Idea

The equation $$ xy = k $$ means the product of $$ x $$ and $$ y $$ will always be a constant. So if one of the variables increases, the other must decrease to compensate. An example of this is summarized in the table below.

Example 1

Suppose $$ xy = 100 $$. Show that as $$ x $$ increases, $$ y $$ must decrease.

Solution

$$ \begin{align*} \begin{array}{ccr@{=}l} x & y & {xy}\hspace{10mm} \\[6pt] \hline 1 & 100 & 1(100)=100\\ 2 & 50 & 2(50)=100\\ 4 & 25 & 4(25)=100\\ 5 & 20 & 5(20)=100\\ 10 & 10 & 10(10)=100\\ 20 & 5 & 20(5)=100\\ 25 & 4 & 25(4)=100\\ 50 & 2 & 50(2)=100\\ 100 & 1 & 100(1)=100\\ 200 & 1/2 & 200(1/2)=100\\ 300 & 1/3 & 300(1/3)=100\\ 400 & 1/4 & 400(1/4)=100\\ \vdots & \vdots & {\vdots} \hspace{10mm} \end{array} \end{align*} $$

Notice that as $$ x $$ is growing larger, the values of $$ y $$ are growing smaller.

Changing Magnitudes

Above, we said that as one variable "gets larger" the other "gets smaller." More precisely, it is their magnitudes that get larger or smaller. You can think of the term magnitude as meaning "size" or "distance from zero." So the numbers $$ 3 $$ and $$ -3 $$ both have the same "magnitude."

Let's look at a variation of the previous example to see how this works.

Example 2

Suppose $$ xy = -100 $$. Show that as $$ x $$ increases, the magnitude of $$ y $$ decreases. That is, $$ y $$ will get closer to zero.

Solution

$$ \begin{align*} \begin{array}{ccr@{=}l} x & y & {xy}\hspace{13mm} \\[6pt] \hline 1 & -100 & 1(-100)=-100\\ 2 & -50 & 2(-50)=-100\\ 4 & -25 & 4(-25)=-100\\ 5 & -20 & 5(-20)=-100\\ 10 & -10 & 10(-10)=-100\\ 20 & -5 & 20(-5)=-100\\ 25 & -4 & 25(-4)=-100\\ 50 & -2 & 50(-2)=-100\\ 100 & -1 & 100(-1)=-100\\ 200 & -1/2 & 200(-1/2)=-100\\ 300 & -1/3 & 300(-1/3)=-100\\ 400 & -1/4 & 400(-1/4)=-100\\ \vdots & \vdots & {\vdots} \hspace{15mm} \end{array} \end{align*} $$

Notice that as $$ x $$ is getting farther from zero, $$ y $$ is getting closer to zero.

This idea that $$ x $$ and $$ y $$ vary inversely in magnitude can easily be seen in a graph of their relationship, as shown below.

As the x moves away from the y-axis, the y-values get close to the x-axis.

As the x moves closer to the y-axis, the y-values get farther to the x-axis.

Function Form

Often, we use the form $$ y = \frac k x $$ when working with inverse variations. This let's us figure out $$ y $$ when we know $$ x $$.

Example 3

Suppose $$ y = \frac{0.3} x $$. Determine the value of $$ y $$ for $$ x = -10, -4, -1/2, -1/5, 1/8, 1/3, 2, 6 $$, and $$ 15 $$.

Solution

$$ \begin{align*} %\arraycolsep=1.4pt \def\arraystretch{1.5} \begin{array}{c|l@{\,=\,}l@{\,=\,}l} x & {y = \frac{0.3} x}\\ \hline -10 & y = \frac{0.3}{-10} \hspace{1mm} = -\frac 3{100} = -0.03\\ -4 & y = \frac{0.3}{-4} \hspace{3mm} = -\frac 3 {40} \hspace{1mm} = -0.075\\ -1/2 & y = \frac{0.3}{-1/2} = -\frac 6 {10} \hspace{1mm} = -\frac 3 5 = -0.6\\ -1/5 & y = \frac{0.3}{-1/5} = -\frac{15}{10} \hspace{1mm} = \frac 3 2 = -1.5\\ 1/8 & y = \frac{0.3}{1/8} \hspace{2mm} = \frac{24}{10} \hspace{5mm} = \frac{12} 5 = 2.4\\ 1/3 & y = \frac{0.3}{1/3} \hspace{2mm} = \frac 9 {10} \hspace{5mm} = 0.9\\ 2 & y = \frac{0.3} 2 \hspace{2mm} = \frac 3 {20} \hspace{5mm} = 0.15\\ 6 & y = \frac{0.3} 6 \hspace{2mm} = \frac 3 {60} \hspace{5mm} = \frac 1 {20} = 0.05\\ 20 & y = \frac{0.3}{15} \hspace{2mm} = \frac 3 {150} \hspace{4mm} = \frac 1 {50} = 0.02 \end{array} \end{align*} $$

Word Problems

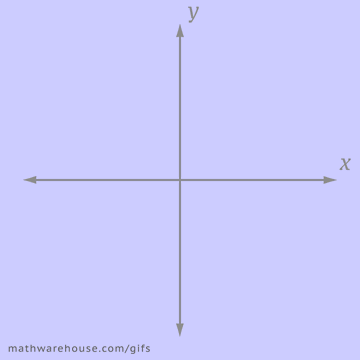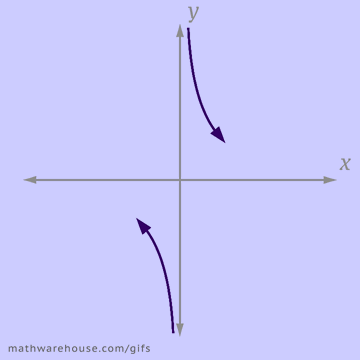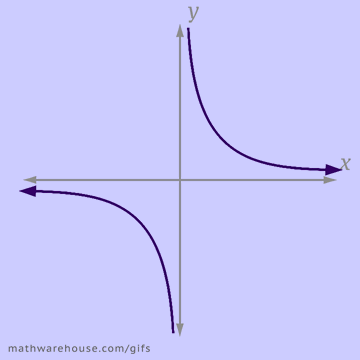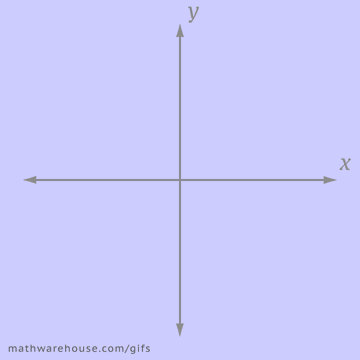
When it comes to applications, or word problems, that involve inverse variation you should keep these things in mind.

Questions will often contain one of these phrases: "varies inversely", "varies indirectly", or "inversely proportional".
Often, the value of $$ k $$ is not given but has to be determined from the data given.
First, find $$ k $$ and then use it to answer the final question.

Example 4

The size of a particular colony of bacteria varies indirectly with temperature. When temperature is held at a constant $$ 30^\circ C $$, the colony contains 4 million bacteria. How many bacteria can survive when the temperature rises to $$ 50^\circ C $$?

Step 1

Define variables.

Since the two quantities being measured in this scenario are bacteria and temperature, let's use

$$ B = $$ number of bacteria, measured in millions. So $$ B = 4 $$ represents 4 million bacteria.
$$ T = $$ temperature, measured in degrees celsius.

Step 2

Use $$ \red{B = 4} $$ and $$ \blue{T = 30} $$ to determine the value of the constant of proportionality, $$ k $$. Then write the updated variation equation.

$$ \begin{align*} \red{B} & = \frac k {\blue T}\\[6pt] \red{4} & = \frac k {\blue{30}}\\[6pt] \red{4}(\blue{30}) & = \frac k {\blue{30}}\cdot \blue{30}\\[6pt] 120 & = \frac k {\cancelred{30}}\cdot\cancelred{30}\\[6pt] k & = 120 \end{align*} $$

The updated variation equation is $$ B = \frac{120}{T} $$.

Step 3

Determine the number of bacteria that can survive when the temperature is $$ \blue{50} $$.

$$ B = \frac{120}{\blue{50}} = \frac{12} 5 = 2.4 $$

Answer

$$ 2{,}400{,}000 $$ bacteria can survive at a temperature of $$ 50^\circ C $$.

Inverse Variation with Non-linear $$ x $$

Sometimes $$ y $$ doesn't vary inversely as "just" $$ x $$, but rather a function of $$ x $$. The language used to describe such problems and the procedures followed to solve them are the same, you just need to read the statements carefully to make sure you have the correct relationships.

Example 5

Suppose $$ y $$ varies inversely as the square of $$ x $$. If $$ y = 5 $$ when $$ x = 3 $$, what is the value of $$ y $$ when $$ x = 1/4 $$?

Step 1

Use $$ \red{y = 5} $$ and $$ \blue{x = 3} $$ to find the value $$ k $$. Then write down the updated variation equation.

$$ \begin{align*} \red y & = \frac k {\blue{x}^2}\\[6pt] \red{5} & = \frac k {\blue{3}^2}\\[6pt] \red{5}(\blue{9}) & = \frac k {\blue{9}}\cdot\blue{9}\\[6pt] 45 & = \frac k {\cancelred{9}}\cdot\cancelred{9}\\[6pt] k & = 45 \end{align*} $$

So now we know $$ y = \frac{45}{x^2} $$.

Step 2

Determine the value of $$ y $$ when $$ \blue{x = 1/4} $$.

$$ \begin{align*} y & = \frac{45}{\blue{x}^2}\\[6pt] y & = \frac{45}{\left(\blue{1/4}\right)^2}\\[6pt] & = \frac{45}{1/16}\\[6pt] & = (45)(16)\\[6pt] & = 720 \end{align*} $$

Answer

$$ y = 720 $$ when $$ x = 1/4 $$.

Practice Problems