Mathwarehouse Logo
reflections over axis, 322x22

Reflect a Point

Across x axis, y axis and other lines

A reflection is a kind of transformation. Conceptually, a reflection is basically a 'flip' of a shape over the line of reflection.

Reflections are opposite isometries, something we will look below.

Reflections are Isometries

Reflections are isometries . As you can see in diagram 1 below, $$ \triangle ABC $$ is reflected over the y-axis to its image $$ \triangle A'B'C' $$. And the distance between each of the points on the preimage is maintained in its image

Diagram 1

reflections are isometries

The length of each segment of the preimage is equal to its corresponding side in the image .

$ m \overline{AB} = 3 \\ m \overline{A'B'} = 3 \\ \\ m \overline{BC} = 4 \\ m \overline{B'C'} = 4 \\ \\ m \overline{CA} = 5 \\ m \overline{C'A'} = 5 $

Though a reflection does preserve distance and therefore can be classified as an isometry, a reflection changes the orientation of the shape and is therefore classified as an opposite isometry.

You can see the change in orientation by the order of the letters on the image vs the preimage. In the orignal shape (preimage), the order of the letters is ABC, going clockwise.

On other hand, in the image, $$ \triangle A'B'C' $$, the letters ABC are arranged in counterclockwise order.

Diagram 2
reflections are not direct isometries animation

Formula List

Reflect over
  • x-axis $$ (a,b) \rightarrow (a, \red - b)$$
    • Ex. $$(3,4) \rightarrow (3 ,\red - 4) $$
  • y-axis $$ (a,b) \rightarrow (\red - a, b)$$
    • Ex. $$(3,4) \rightarrow (\red - 3 ,4) $$
  • line $$y = x $$ $$ (a,b) \rightarrow (b, a)$$
    • Ex. $$(3,4) \rightarrow (4, 3) $$
  • line $$y = -x $$ $$ (a,b) \rightarrow (\red - b, \red - a )$$
    • Ex. $$(3,4) \rightarrow (\red - 4 ,\red - 3) $$

Most Common Types of Reflections

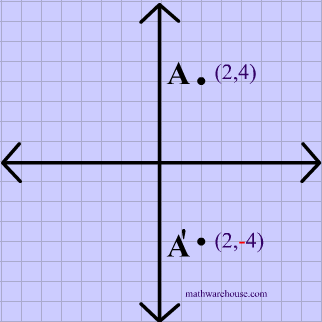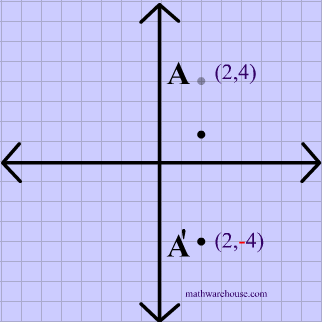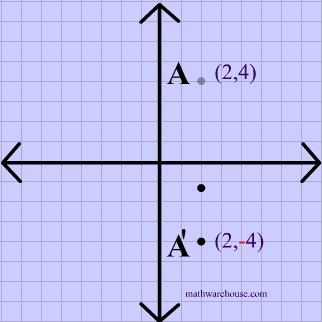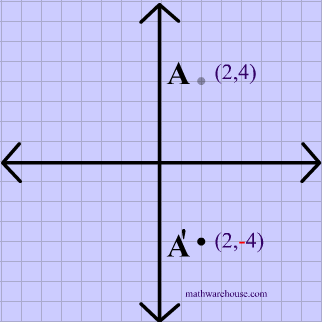
Reflection over the x-axis

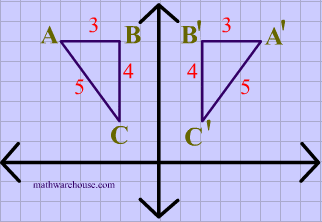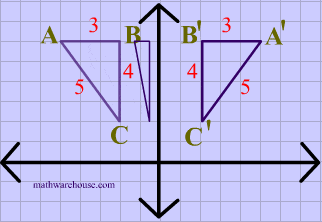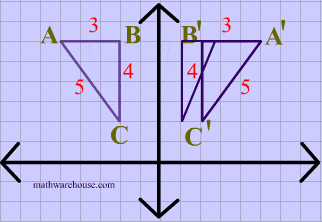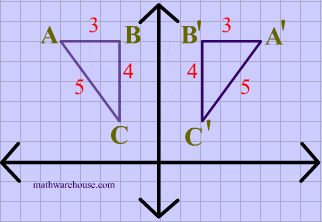
A reflection over the x-axis can be seen in the picture below in which point A is reflected to its image A'. The general rule for a reflection over the x-axis:

$ (A,B) \rightarrow (A, -B) $

Diagram 3
Applet 1
y =
m
x +
c
You can drag the point anywhere you want

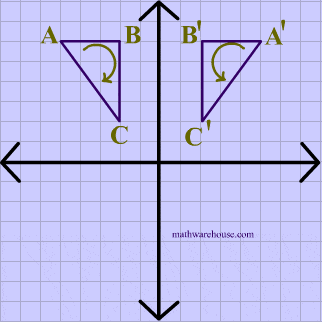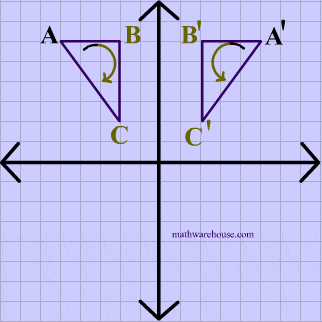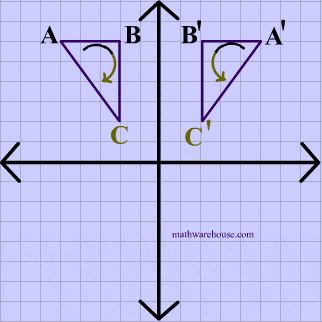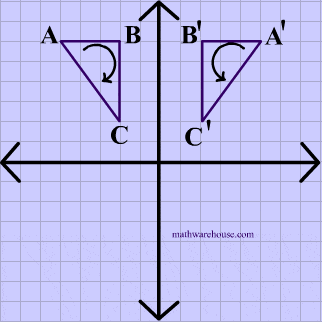
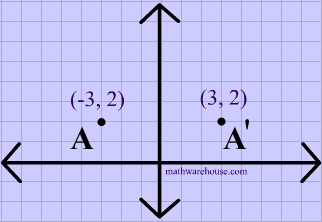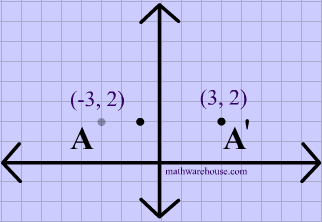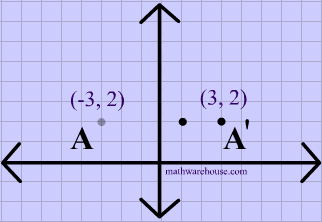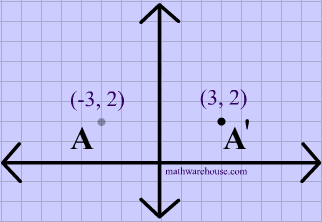
Reflection over the y-axis

A reflection in the y-axis can be seen in diagram 4, in which A is reflected to its image A'. The general rule for a reflection over the y-axis

$ r_{y-axis} \\ (A,B) \rightarrow (-A, B) $

Diagram 4
Applet
y =
m
x +
c
You can drag the point anywhere you want
Diagram 5

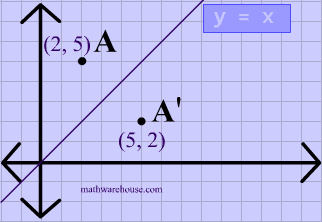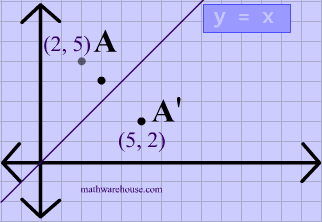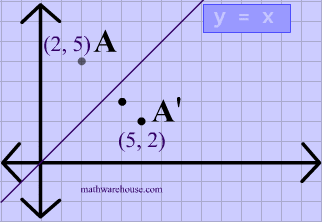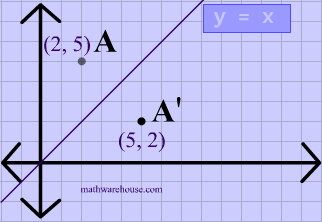
Reflection over the line $$ y = x $$

A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A'.

The general rule for a reflection in the $$ y = x $$ :

$ (A,B) \rightarrow (B, A ) $

Applet
y =
m
x +
c
You can drag the point anywhere you want

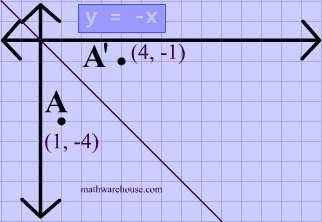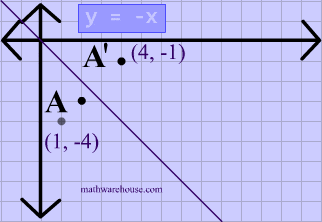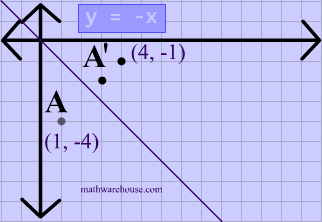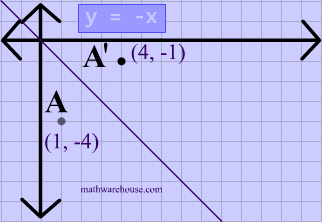
Reflection over the line $$ y = -x $$

A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A'.

The general rule for a reflection in the $$ y = -x $$ :

$ (A,B) \rightarrow (\red - B, \red - A ) $

Diagram 6
Applet
y =
m
x +
c
You can drag the point anywhere you want

Reflections Applet

y =
m
x +
c

Select Reflection Line

Select Shape To reflect

Select If You Want Auto Flip For Shapes

Or Use This Button To Flip

Practice Problems

Perform the reflections indicated below

Problem 1

What is the image of point A(1,2) after reflecting it across the x-axis. In technical speak, pefrom the following transformation r(x-axis)?

Picture of reflection across y axis
Problem 2

What is the image of point A (31,1) after reflecting it across the x-axis. In technical speak, pefrom the following transformation r(y-axis)?

Picture of reflection across y axis
Problem 3

What is the image of point A(-2,,1) after reflecting it across the the line y = x. In technical speak, pefrom the following transformation r(y=x)?

Picture of reflection across y axis

Problems II

Problem 4

Point Z is located at $$ (2,3) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the x-axis

Remember to reflect over the x-axis , just flip the sign of the y coordinate.
$ (2,3) \rightarrow (2 , \red{-3}) $
Problem 5

Point Z is located at $$ (-2, 5) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the line $$y=x$$

Remember to reflect over the line y =x , you just swap the x and y coordinate values.
$ ( -2 , 5 ) \rightarrow ( 5 , -2 ) $
Problem 6

Point Z is located at $$ (-11,7) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the y-axis

Remember to reflect over the y-axis , you just flip the sign of the x coordinate.
$ ( -8 ,7 ) \rightarrow ( \red 8 , 7 ) $
Problem 7

Point Z is located at $$ (-3, -4 ) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the x-axis

Remember to reflect over the x-axis , just flip the sign of the y coordinate.
$ (-3, -4 ) \rightarrow (-3 , \red{4}) $
Back to Transformations Next to Point Reflections

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!