How to Evaluate a Function, Function notation, Input ,Output, Visual Examples and explained problems

How do you evaluate functions?

The same way that you substitute values into equations!

Example 1

What is the value of $$ x $$ given the equation $$ y = 2x $$ when $$ x = 5 $$?

Substitute '5' in for x :

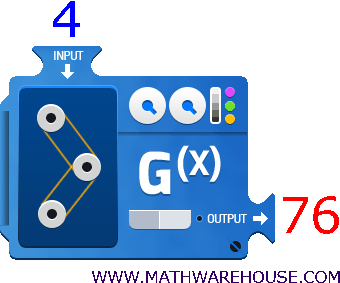
The one new aspect of function notation is the emphasis on input and output .

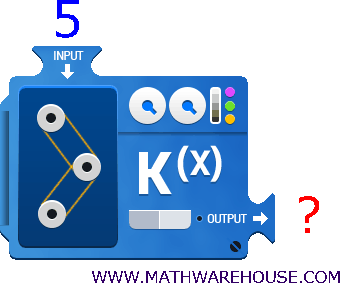
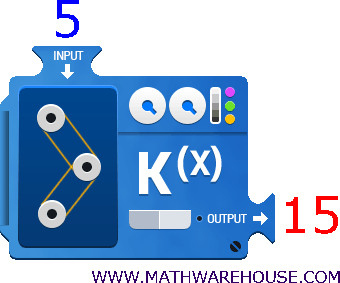
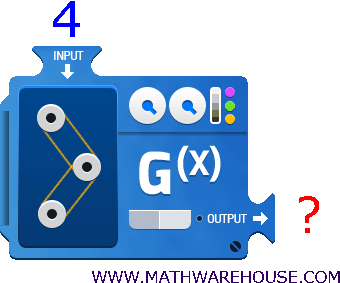
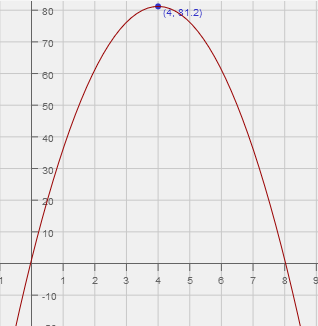
example of how to evaluate a function in math

Example 2

What is the value of $$ x $$ given the equation $$ y = x-5 $$ when $$ x = 7 $$?

Substitute '7' in for x :

Again, this new way involves an input and output .

Function Machine

You can think of $$ f(x)$$ as a function machine. The function machine, or $$ f(x)$$ , takes input inside. The machine processes this input and produces an output value

Practice Problems

Problem 1

Let $$ k(x) =3x $$.

Evaluate $$ k (5) $$.

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ k(\blue{x }) =3 \blue{x } \\ k(\blue{5 }) =3\cdot \blue{5 } $$

Step 2

Compute result.

$$ k(\blue5 ) =3\cdot \blue 5 \\ = \red {15} $$

$$ k(\blue {input }) =\red {output} \\ k(\blue 5) =\red {15} $$

Problem 2

Let $$ g(x) =3x^2 + 7x $$.

Evaluate $$ g(4) $$.

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ g(\blue x ) =3 \blue x ^2 + 7 \blue x \\ g(\blue 4 ) =3\cdot \blue 4 ^2 + 7\cdot \blue 4 $$

Step 2

Compute result.

$$ g(\blue 4 ) =3\cdot \blue 4 ^2 + 7\cdot \blue 4 \\ g(\blue 4 ) = \red{76} $$

$$ g(\blue {input }) =\red {output} \\ g(\blue 4) =\red {76} $$

Problem 3

Let $$ h(x) =\sqrt{x^3 -4}-|x| $$.

Evaluate $$ h(5) $$.

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ h(\blue x ) = \sqrt{\blue x ^3 -4}-| \blue{x }| \\ h(\blue {5 }) = \sqrt{\blue 5 ^3 - 4 } - | \blue 5 | $$

Step 2

Compute result.

$$ h(\blue 5 ) = \sqrt{\blue 5 ^3 -4}-|\blue 5 | \\ h(\blue 5 ) =50 \\ h(\blue 5) = \red 6 $$

$$ h(\blue {input }) =\red {output} \\ h(\blue 5) =\red 6 $$

Problem 4

Let $$ f(x) = -3x^2 + 5x - 1 $$.

Evaluate $$ f(6) $$.

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ f(\blue x ) = -3 \blue x ^2 + 5\blue x - 1 \\ f(\blue 6 ) = -3 \cdot \blue 6 ^2 + 5\cdot \blue 6 - 1 $$

Step 2

Compute result.

$$ f(\blue 6 ) = -3 \cdot \blue 6^2 + 5\cdot \blue 6 - 1 \\ f(\blue 6) = \red{-79} $$

$$ f(\blue {input }) =\red {output} \\ f(\blue 6) =\red {-79} $$

Problem 5

The height in meters of a projectile at t seconds can be found by the function $$ h(t) = -5t^2 + 40t + 1.2 $$.

Find the height of the projectile 4 seconds after it is launched.

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ h(\blue t ) = -5\blue t^2 + 40 \blue t + 1.2 \\ h(\blue 4 ) = -5 \cdot \blue 4 ^2 + 40 \cdot \blue 4 + 1.2 $$

Step 2

Compute result.

$$ h(\blue 4 ) = -5 \cdot \blue 4^2 + 40 \cdot \blue 4 + 1.2 \\ h(\blue 4 ) = \red{81.2} $$

$$ h(\blue {input }) =\red {output} \\ h(\blue 4) =\red {81.2} $$

Here is a picture of graph of projectile's path with the point $$ (\blue {t}, \red{h(t)}) (\blue 4, \red {81.2}) $$ :

Problem 6

A substance has a half life of 26 years. The amount of remaining substance in grams after t years can be found by the function $$ h(t) = 250 (0.5)^{ \frac{t}{25} } $$.

How much substance remains after 98 years?

Step 1

Identify all of the occurrences of 'x' and substitute the input in

$$ h(\blue t) = 250 (0.5)^{ \frac{\blue t}{25} } \\ h(\blue { 98 }) = 250 (0.5)^{ \frac{\blue{98}}{25} } $$

Step 2

Compute result.

$$ h(\blue{98}) = 250 (0.5)^{ \frac{\blue{98}}{25} } \\ h(\blue{98}) = \red{16.5159} $$

$$ h(\blue {input }) =\red {output} \\ h(\blue {98}) =\red {16.5159} $$

Here is a picture of graph of projectile's path with the point $$ (\color{blue} {t}, \color{red} {h(t)}) (\color{blue} {98} , \color{red} {16.5159}) $$ :.